시작시간 = [2025-11-21 21:49:03.0167]
req=[org.apache.catalina.connector.RequestFacade@62520d71]
res=[org.apache.catalina.connector.ResponseFacade@78f0a824]
conn=[com.mysql.jdbc.JDBC4Connection@7156091c]
cdAry[0] = []
cdAry[1] = [TABLE 1.1) String uAry[][]
query[0] = Select sid, SYMBOL, UNIT, DESCR, kid From S_DATA Where kid=6 and sid=0
| sid | SYMBOL | UNIT | DESCR | kid |
| 0 | PUnit | bar | 1 | bar | 입력 압력단위 (Pressue Input Unit) = bar | | 6 |
]
cdAry[2] = [TABLE 2.1) String bAry[][] = S_RESULT
query[1] = Select sid, DESCR, UNIT, SYMBOL, T1,T2,T3,T4,T5,T6,T7,T8,T9,T10,REMARK From S_RESULT Where kid=6 and sid<100 Order By sid
| sid | DESCR | UNIT | SYMBOL | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | T10 | REMARK |
| 0 | Nominal Capacity [공칭용량] | m³ | V_nom | 2006.970 | 2006.970 | 8379.160 | ||||||||
| 1 | Storage Capacity [저장용량] | m³ | V_sto | 1950.430 | 1950.430 | 7541.290 | ||||||||
| 2 | Vapor Space Capacity | m³ | V_hil | 56.540 | 56.540 | 837.870 | ||||||||
| 3 | Storage Capacity Ratio | % | R_Sto | 97.180 | 97.180 | 90.000 | ||||||||
| 4 | Vapor Space Ratio | % | R_vapor | 2.820 | 2.820 | 10.000 | ||||||||
| 10 | A. WEIGHT SUMMARY | |||||||||||||
| 11 | SHELL PLATE | Ton | Ws | 166.145 | 157.566 | 541.785 | ||||||||
| 12 | UPPER COLUMN (PLATE) | Ton | Wuc | 6.653 | 6.648 | 32.426 | ||||||||
| 13 | LOWER COLUMN (PIPE) | Ton | Wc | 13.096 | 13.099 | 56.831 | ||||||||
| 14 | CROSS BRACE (PIPE) | Ton | Wb | 11.397 | 11.397 | 21.319 | ||||||||
| 15 | ROOF PLATFORM & STAIRWAY | Ton | Wr | 11.786 | 11.789 | 51.148 | ||||||||
| 16 | WATER SPRAY AND ATTACHMENT | Ton | Wsp | 10.477 | 10.479 | 45.465 | ||||||||
| 17 | MANHOLE & NOZZLE | Ton | Wn | 12.200 | 12.200 | 19.500 | ||||||||
| 18 | INTERNAL LADDER & ATTACHMENT | Ton | Wi | 9.626 | 9.626 | 15.386 | ||||||||
| 19 | ANCHOR BOLT/NUT | Ton | Wa | 3.180 | 3.180 | 4.452 | ||||||||
| 20 | COLUMN FIRE PROOFING | Ton | Win | 30.200 | 30.200 | 70.500 | ||||||||
| 21 | BLANK 1 | Ton | W_1 | |||||||||||
| 22 | BLANK 2 | Ton | W_2 | |||||||||||
| 23 | BLANK 3 | Ton | W_3 | |||||||||||
| 24 | BLANK 4 | Ton | W_4 | |||||||||||
| 25 | BLANK 5 | Ton | W_5 | |||||||||||
| 26 | Lower-Column O.D | mm | Dcol | 609.600 | 609.600 | 1066.800 | ||||||||
| 27 | Lower-Column Thickness | mm | Tcol | 12.700 | 12.700 | 16.000 | ||||||||
| 28 | Cross-Brace O.D | mm | Dbrace | 219.100 | 219.100 | 219.100 | ||||||||
| 29 | Cross-Brace Thickness | mm | Tbrace | 12.700 | 12.700 | 12.700 | ||||||||
| 30 | ■ EMPTY WEIGHT (1 Unit) | Ton | We | 274.760 | 266.180 | 858.810 | We = W(1)+ .. +W(10) | |||||||
| 31 | B. LOADING DATA | |||||||||||||
| 32 | CONTENTS WEIGHT (at Operating) | Ton | Wc | 1212.190 | 1212.190 | 4449.360 | Wc = Vsto * S.G | |||||||
| 33 | HYDROSTATIC TEST WATER WEIGHT | Ton | Wt | 2006.970 | 2006.970 | 8379.160 | Wt = Vnom * 1.0 | |||||||
| 34 | 1) VERTICAL LOAD | |||||||||||||
| 35 | EMPTY WEIGHT | Ton | We | 274.760 | 266.180 | 858.810 | We = W(1)+ .. +W(10) | |||||||
| 36 | OPERATING WEIGHT | Ton | Wo | 1486.950 | 1478.370 | 5308.170 | Wo = We + Wc | |||||||
| 37 | HYDROSTATIC TEST WEIGHT | Ton | Wh | 2281.730 | 2273.150 | 9237.970 | Wh = We + Wt | |||||||
| 38 | 2) HORIZONTAL LOAD | |||||||||||||
| 39 | SEISMIC FACTOR (CS=0.25 Fix) | CS | 0.250 | 0.250 | 0.250 | |||||||||
| 40 | SEISMIC LOAD (Base Shear) Vs = CS x Wo | Ton | Vs | 371.740 | 369.590 | 1327.040 | Vs = CS x Wo | |||||||
| 41 | WIND LOAD (Base Shear) | Ton | Vw |
]
cdAry[3] = [TABLE 3.1) String cAry[][] = S_DETAIL, cAry.length = [36] cAry[0].length = [12]
query[2] = Select sid, SYMBOL, T1,T2,T3,T4,T5,T6,T7,T8,T9,T10 From S_DETAIL Where kid=6 and sid<100 Order By sid
| sid | SYMBOL | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | T10 |
| 1 | TNO | V-1110A/B | V-1110A/B | V-1110A/B | |||||||
| 2 | CODE | DIV. 1 | DIV. 1 | DIV. 2 | |||||||
| 3 | CONTENT | 1,3 Butane | 1,3 Butane | Propylene | |||||||
| 4 | SG | 0.6215 | 0.6215 | 0.59 | |||||||
| 5 | MATL | SA516-70 | SA516-70 | SA537-CL2 | |||||||
| 6 | DTEMP | 68 | 68 | 68 | |||||||
| 7 | Sd | 138.00 | 138.00 | 230.00 | |||||||
| 8 | Di | 15650 | 15650 | 25200 | |||||||
| 9 | CA | 3.0 | 3.0 | 1.5 | |||||||
| 10 | HT | 10825 | 10825 | 15600 | |||||||
| 11 | HHLL | 14080 | 14080 | 20266 | |||||||
| 12 | HLL | 12520 | 12520 | 20266 | |||||||
| 13 | LLL | 2000 | 2000 | 2000 | |||||||
| 14 | LLLL | 1000 | 1000 | 1000 | |||||||
| 15 | Pi | 6.0 | 6.0 | 8.335653 | |||||||
| 16 | Pe | 1.01325 | 1.01325 | 1.01325 | |||||||
| 17 | MDMT | -19 | -19 | -19 | |||||||
| 18 | E | 0.8 | 1.0 | 1.0 | |||||||
| 19 | TQTY | 1.0 | 1.0 | 1.0 | |||||||
| 20 | CQTY | 10 | 10 | 14 | |||||||
| 21 | SQTY | 8 | 8 | 10 | |||||||
| 22 | CACB | 3.0 / 3.0 | 3.0 / 3.0 | 3.0 / 3.0 | |||||||
| 23 | L | 64.0 | 64.0 | 64.0 | |||||||
| 24 | tdReq | 27.33 | 22.46 | 27.57 | |||||||
| 25 | twReq | 15.62 | 15.62 | 20.62 | |||||||
| 26 | tmReq | 15.62 | 15.62 | 21.29 | |||||||
| 27 | teReq | 25.25 | 25.25 | 33.71 | |||||||
| 28 | tTops | 26.0 | 26.0 | 34.5 | |||||||
| 29 | tMids | 27.5 | 26.0 | 34.5 | |||||||
| 30 | tBtms | 28.5 | 26.0 | 34.5 | |||||||
| 31 | tUsed | 28.5 | 26.0 | 34.5 | |||||||
| 32 | MSG | OK | OK | OK | |||||||
| 33 | tdCyo | 51.81 | 42.02 | 53.7 | |||||||
| 34 | ttCyt | 34.3 | 34.3 | 44.11 | |||||||
| 35 | tCyli | 53.0 | 43.0 | 54.5 |
]
cdAry[4] = [[cAry, dAry] TANK STRENGTH CALCULATION SHEET, uid= [1], units= [bar]
| 1 | 1 | TANK NO. (Max. 40 Char.) | TNO = | V-1110A/B 0 | V-1110A/B 0 | V-1110A/B 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 2 | VESSEL DESIGN CODE (ASME SEC. VIII, Div. 1,2) | CODE = | DIV. 1 1 | DIV. 1 1 | DIV. 2 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 3 | STORAGE LIQUID NAME | CONTENT = | 1,3 Butane 0 | 1,3 Butane 0 | Propylene 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 4 | DESIGN SPECIFIC GRAVITY | SG = | 0.6215 0.6215 | 0.6215 0.6215 | 0.59 0.59 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 5 | MATERIAL OF SHELL PLATE | MATL = | SA516-70 0 | SA516-70 0 | SA537-CL2 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 6 | DESIGN TEMPERATURE (Max.) | DTEMP = | ℃ | 68 68 | 68 68 | 68 68 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 7 | ALLOWABLE STRESS at Deisin(Operating) | Sd = | MPa | 138.00 138 | 138.00 138 | 230.00 230 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 8 | TANK INSIDE DIAMETER | Di = | mm | 15650 15650 | 15650 15650 | 25200 25200 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 9 | CORROSION ALLOWANCE (SHELL) | CA = | mm | 3.0 3 | 3.0 3 | 1.5 1.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 10 | TANK EQUATOR LEVEL (FROM GROUND) | HT = | mm | 10825 10825 | 10825 10825 | 15600 15600 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | 11 | (SHELL 두께계산 높이) HIGH HIGH LIQUID LEVEL | HHLL = | mm | 14080 14080 | 14080 14080 | 20266 20266 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | 12 | (Storage 용량계산 액높이) HIGH LIQUID LEVEL | HLL = | mm | 12520 12520 | 12520 12520 | 20266 20266 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | 13 | LOW LIQUID LEVEL | LLL = | mm | 2000 2000 | 2000 2000 | 2000 2000 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | 14 | LOW LOW LIQUID LEVEL | LLLL = | mm | 1000 1000 | 1000 1000 | 1000 1000 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | 15 | DESIGN INTERNAL PRESSURE (DATA SHEET 상의 압력) 프로그램이 계산시 사용하는 압력은? [SI UNIT] | Pi = | bar kPa | 6.0 600 | 6.0 600 | 8.335653 833.5653 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | 16 | DESIGN EXTERNAL PRESSURE (DATA SHEET 상의 압력) 프로그램이 계산시 사용하는 압력은? [SI UNIT] | Pe = | bar kPa | 1.01325 101.325 | 1.01325 101.325 | 1.01325 101.325 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | 17 | MIN.DESIGN METAL TEMPERATURE | MDMT = | ℃ | -19 -19 | -19 -19 | -19 -19 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | 18 | SHELL JOINT EFFICIENCY | E = | 0.8 0.8 | 1.0 1 | 1.0 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | 19 | TANK QUANTITY (탱크수량 직접입력) | TQTY = | Unit | 1.0 1 | 1.0 1 | 1.0 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | 20 | COLUMN QUANTITY (수량자동계산) | CQTY = | EA | 10 10 | 10 10 | 14 14 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | 21 | SHELL SEGMENT QUANTITY (수량자동계산) | SQTY = | EA | 8 8 | 8 8 | 10 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | 22 | CORROSION ALLOWANCE (Column/Brace) | CACB = | mm | 3.0 / 3.0 0 | 3.0 / 3.0 0 | 3.0 / 3.0 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | 23 | Cylinderical Vessel Longitudinal Length ex) Mounded Bullet Vessel(Cylinderical) Length | L = | (m) | 64.0 64 | 64.0 64 | 64.0 64 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | 24 | Req'd Thickness under Operating Cond. (Pi+Ps) | tdReq = | mm | 27.33 27.33 | 22.46 22.46 | 27.57 27.57 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | 25 | Req'd Thickness under Hydro-test (MAWP) (Pt) | twReq = | mm | 15.62 15.62 | 15.62 15.62 | 20.62 20.62 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | 26 | Req'd Thickness under Hydro-test (MAP) (Pt) | tmReq = | mm | 15.62 15.62 | 15.62 15.62 | 21.29 21.29 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | 27 | Req'd Thickness under External Pressue (Pe) | teReq = | mm | 25.25 25.25 | 25.25 25.25 | 33.71 33.71 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | 28 | ● Top Shell Used Thickness | tTops = | mm | 26.0 26 | 26.0 26 | 34.5 34.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | 29 | ● Equator Used Thickness | tMids = | mm | 27.5 27.5 | 26.0 26 | 34.5 34.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | 30 | ● Bottom Shell Used Thickness | tBtms = | mm | 28.5 28.5 | 26.0 26 | 34.5 34.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | 31 | ● Max. (Spherical) Used Thickness | tUsed = | mm | 28.5 28.5 | 26.0 26 | 34.5 34.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | 32 | If (tUsed ≤ 64mm) then Accetable Else (tUsed>64mm) Sd ReSelect | MSG = | OK 0 | OK 0 | OK 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | 33 | (● Cylinder) Req'd Thickness under Oper. (Pi+Ps) | tdCyo = | mm | 51.81 51.81 | 42.02 42.02 | 53.7 53.7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | 34 | (● Cylinder) Req'd Thickness under Hydrotest(Pt) | ttCyt = | mm | 34.3 34.3 | 34.3 34.3 | 44.11 44.11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | 35 | ● Max. (Cylinder) Used Thickness | tCyli = | mm | 53.0 53 | 43.0 43 | 54.5 54.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Weight Summary and SITE Welding Length | Strength Calculation Result, sWt[][][] | ||||||||||||||||||
| No. | Each Angle θ, deg | Sum Angle φ, deg | Shell Thk mm | Shell Width mm | Shell Length mm | Qty SHT | Net Weight kg | 수평용접부 단면경 øD, mm | 수평용접 hWeld L=øD,mm | 수직용접 vWeld L, mm | Shell Thk mm | Width mm | Length mm | Qty Sht | Unit WT kg/sht | Net Weight kg | 각단 높이 mm | 표면적 A=πD*m (m²) | |
| #1, 0 | 10 | 10 | 26.5 | 2731.4 | 8194.3 | 1 | 4,423 | 16,389 | 26.5 | 2731.4 | 8194.3 | 3 | 4423.24 | 13269.7 | 1048.35 | 63.789 | |||
| #2, 0 | 20 | 30 | 26.5 | 2731.4 | 7256.1 | 2 | 8,846 | ø7825 | 29,024 | 5,883 | |||||||||
| #3, 3 | 20 | 50 | 26.5 | 2731.4 | 9415.8 | 4 | 15,319 | ø11988.6 | 37,663 | 26.5 | 2731.4 | 8677.2 | 4 | 3829.69 | 15318.8 | 1746.84 | 73.639 | ||
| #4, 4 | 16 | 66 | 26.5 | 7485.9 | 2185.2 | 6 | 18,892 | ø14297 | 44,915 | 13,111 | 26.5 | 2495.3 | 8194.3 | 6 | 3148.60 | 18891.6 | 1847.1 | 90.814 | |
| #5, 5 | 64 | 130 | 27.5 | 2731.4 | 8848.6 | 18 | 87,165 | ø15650 | 157,331 | 27.5 | 2731.4 | 8848.6 | 18 | 4842.51 | 87165.1 | 8212.52 | 403.776 | ||
| #6, 8 | 20 | 150 | 28.0 | 2731.4 | 9415.8 | 4 | 16,186 | ø11988.6 | 37,663 | 28.0 | 2731.4 | 8477.2 | 4 | 4046.46 | 16185.9 | 1746.84 | 73.639 | ||
| #7, 9 | 20 | 170 | 28.5 | 2731.4 | 7256.1 | 2 | 9,514 | ø7825 | 29,024 | 5,883 | 28.5 | 2731.4 | 8194.3 | 3 | 4757.06 | 14271.2 | 1048.35 | 63.789 | |
| #8, 9 | 10 | 180 | 28.5 | 2731.4 | 8194.3 | 1 | 4,757 | 16,389 | |||||||||||
| Total Quantity and Shell Weight | 38 | 165,102 | kg | 211.1 (m) | 182.2 (m) | 38 | 165102.2 | 15650.00 | 769.446 | ||||||||||
| Total Site Weleding length (m) | 393.3 (m) | ||||||||||||||||||
CalcRpt[tid][0].length() = [10] Bytes
1. Shell Plate 현장 용접길이 계산, Tank Dia. D = 15,650 (m), Material SA516-70, HEAD TYPE : FOOT BALL
| Weight Summary and SITE Welding Length | Strength Calculation Result, sWt[][][] | ||||||||||||||||||
| No. | Each Angle θ, deg | Sum Angle φ, deg | Shell Thk mm | Shell Width mm | Shell Length mm | Qty SHT | Net Weight kg | 수평용접부 단면경 øD, mm | 수평용접 hWeld L=øD,mm | 수직용접 vWeld L, mm | Shell Thk mm | Width mm | Length mm | Qty Sht | Unit WT kg/sht | Net Weight kg | 각단 높이 mm | 표면적 A=πD*m (m²) | |
| #1, 0 | 10 | 10 | 26.5 | 2731.4 | 8194.3 | 1 | 4,423 | 16,389 | 26.5 | 2731.4 | 8194.3 | 3 | 4423.24 | 13269.7 | 1048.35 | 63.789 | |||
| #2, 0 | 20 | 30 | 26.5 | 2731.4 | 7256.1 | 2 | 8,846 | ø7825 | 29,024 | 5,883 | |||||||||
| #3, 3 | 20 | 50 | 26.5 | 2731.4 | 9415.8 | 4 | 15,319 | ø11988.6 | 37,663 | 26.5 | 2731.4 | 8677.2 | 4 | 3829.69 | 15318.8 | 1746.84 | 73.639 | ||
| #4, 4 | 16 | 66 | 26.5 | 7485.9 | 2185.2 | 6 | 18,892 | ø14297 | 44,915 | 13,111 | 26.5 | 2495.3 | 8194.3 | 6 | 3148.60 | 18891.6 | 1847.1 | 90.814 | |
| #5, 5 | 64 | 130 | 26.5 | 2731.4 | 8848.6 | 18 | 83,996 | ø15650 | 157,331 | 26.5 | 2731.4 | 8848.6 | 18 | 4666.42 | 83995.5 | 8212.52 | 403.776 | ||
| #6, 8 | 20 | 150 | 26.5 | 2731.4 | 9415.8 | 4 | 15,319 | ø11988.6 | 37,663 | 26.5 | 2731.4 | 8477.2 | 4 | 3829.69 | 15318.8 | 1746.84 | 73.639 | ||
| #7, 9 | 20 | 170 | 26.5 | 2731.4 | 7256.1 | 2 | 8,846 | ø7825 | 29,024 | 5,883 | 26.5 | 2731.4 | 8194.3 | 3 | 4423.24 | 13269.7 | 1048.35 | 63.789 | |
| #8, 9 | 10 | 180 | 26.5 | 2731.4 | 8194.3 | 1 | 4,423 | 16,389 | |||||||||||
| Total Quantity and Shell Weight | 38 | 160,064 | kg | 211.1 (m) | 182.2 (m) | 38 | 160064 | 15650.00 | 769.446 | ||||||||||
| Total Site Weleding length (m) | 393.3 (m) | ||||||||||||||||||
CalcRpt[tid][0].length() = [10] Bytes
1. Shell Plate 현장 용접길이 계산, Tank Dia. D = 25,200 (m), Material SA537-CL2, HEAD TYPE : FOOT BALL
| Weight Summary and SITE Welding Length | Strength Calculation Result, sWt[][][] | ||||||||||||||||||
| No. | Each Angle θ, deg | Sum Angle φ, deg | Shell Thk mm | Shell Width mm | Shell Length mm | Qty SHT | Net Weight kg | 수평용접부 단면경 øD, mm | 수평용접 hWeld L=øD,mm | 수직용접 vWeld L, mm | Shell Thk mm | Width mm | Length mm | Qty Sht | Unit WT kg/sht | Net Weight kg | 각단 높이 mm | 표면적 A=πD*m (m²) | |
| #1, 0 | 6.4 | 6.4 | 35.5 | 2814.9 | 8444.6 | 1 | 6,293 | 16,889 | 35.5 | 2814.9 | 8444.6 | 3 | 6293.04 | 18879.1 | 700.86 | 67.746 | |||
| #2, 0 | 12.8 | 19.2 | 35.5 | 2814.9 | 8006.7 | 2 | 12,586 | ø8287.4 | 32,027 | 5,085 | |||||||||
| #3, 3 | 12.8 | 32 | 35.5 | 2814.9 | 10488.2 | 4 | 23,361 | ø13354 | 41,953 | 35.5 | 2814.9 | 9642.7 | 4 | 5840.26 | 23361.0 | 1213.73 | 83.829 | ||
| #4, 4 | 9.5 | 41.5 | 35.5 | 8743.1 | 2089.2 | 6 | 27,546 | ø16698 | 52,458 | 12,535 | 35.5 | 1873.5 | 8796.5 | 9 | 3060.69 | 27546.2 | 1248.57 | 98.847 | |
| #5, 5 | 45.5 | 87 | 35.5 | 2823.6 | 10006 | 28 | 193,649 | ø25165.5 | 79,060 | 280,167 | 35.5 | 2823.6 | 10050 | 28 | 6916.03 | 193648.8 | 8777.41 | 694.891 | |
| #6, 6 | 51.5 | 138.5 | 35.5 | 2827.4 | 11387.8 | 28 | 222,746 | ø25200 | 317,112 | 35.5 | 2827.4 | 11387.8 | 28 | 7955.21 | 222745.8 | 10096.27 | 799.303 | ||
| #7, 9 | 9.5 | 148 | 35.5 | 8743.1 | 2089.2 | 6 | 27,546 | ø16698 | 52,458 | 12,535 | 35.5 | 1873.5 | 8796.5 | 9 | 3060.69 | 27546.2 | 1248.57 | 98.847 | |
| #8, 10 | 12.8 | 160.8 | 35.5 | 2814.9 | 10488.2 | 4 | 23,361 | ø13354 | 41,953 | 35.5 | 2814.9 | 9442.7 | 4 | 5840.26 | 23361.0 | 1213.73 | 83.829 | ||
| #9, 11 | 12.8 | 173.6 | 35.5 | 2814.9 | 8006.7 | 2 | 12,586 | ø8287.4 | 32,027 | 5,085 | 35.5 | 2814.9 | 8444.6 | 3 | 6293.04 | 18879.1 | 700.86 | 67.746 | |
| #10, 11 | 6.4 | 180 | 35.5 | 2814.9 | 8444.6 | 1 | 6,293 | 16,889 | |||||||||||
| Total Quantity and Shell Weight | 82 | 555,967 | kg | 365.7 (m) | 632.5 (m) | 88 | 555967.2 | 25200.00 | 1995.038 | ||||||||||
| Total Site Weleding length (m) | 998.2 (m) | ||||||||||||||||||
CalcRpt[tid][0].length() = [10] Bytes
1. CAPACITY CALCULATION
| 탱크 공칭 및 저장용량 | 하중조건 (Loading Data) | |||||||||||||||
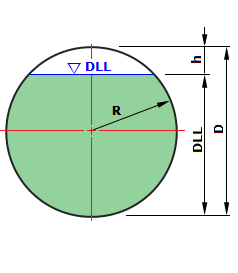
| No | TNO | Liquid Name | SG | D | DLL | Vnom | Vsto | Vhil | vRatio | 탱크 표면적 | 4.Empty Steel | 5,저장 액체 | 6.운전 중량 | 7.수압 수중량 | 8.수압 테스트중량 | |
| mm | mm | m³ | m³ | m³ | (%) | m2 | Ton | |||||||||
| 1 | V-1110A/B | 1,3 Butane | 0.6215 | 15,650 | 14,080 | 2006.97 | 1950.43 | 56.54 | 2.8 (%) | 769.45 | 185.34 | 1212.19 | 1397.53 | 2006.97 | 2192.31 | |
| 2 | V-1110A/B | 1,3 Butane | 0.6215 | 15,650 | 14,080 | 2006.97 | 1950.43 | 56.54 | 2.8 (%) | 769.45 | 180.23 | 1212.19 | 1392.42 | 2006.97 | 2187.21 | |
| 3 | V-1110A/B | Propylene | 0.59 | 25,200 | 20,266 | 8379.16 | 7541.29 | 837.86 | 10 (%) | 1995.04 | 652.5 | 4449.36 | 5101.86 | 8379.16 | 9031.66 | |
| ||||||||||||||||
Ratio of vapour Space, vRatio = Vhil / Vnom * 100(%)
uAry[1][3] = [ 1 | bar | 입력 압력단위 (Pressue Input Unit) = bar | ]
uAry[1][3].substring(0,1).trim() = [1]
uid = [1]
cAry.length = [36] cAry[0].length = [12]
sph.MYANG_SET();
sph.CODE_CALC( );
DESIGN DATA AND MATERIAL LIST
| No. | F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 | F16 | F17 | F18 | F19 | F20 | F21 | F22 | F23 | F24 | F25 | F26 | F27 | F28 | F29 | F30 | F31 | F32 | F33 | F34 | Cylindrical Shell | |||
| No. | TNO | CODE | CONTENT | SG | Di | CA | HT | HHLL | Pi | Pe | MDMT | DTEMP | CQTY | MSG | MATL | Sd | gtReq Used Thk | 6Roark tRoark | 1_ASME tASME | td_2 tTest | td_3 tMAWP | td_5 tMAP | td_5 tVacuum | Shell Qty | Net Weight Ton | Column Qty | Tank Height BASE to EQ. Line (mm) | Upp. Colume Height(mm) | Low. Colume Height(mm) | Column PCD mm | BRACE 부착각도 (o)deg. | Column Size | Shell 각도 분할수 | Spherical Top ~ Btm 두께(mm) | Shell matl id, Sd MPa | Cyl. td (mm) | Cyl. tt (mm) | Cyl. tt(MAWP) (mm) | Cyl. tt(MAP) (mm) |
| 1 | V-1110A/B | DIV. 1 | 1,3 Butane | 0.6215 | 15650 | 3.0 | 10825 | 14080 | 6.0 | 1.01325 | -19 | 68 | 10 | OK | SA516-70 | 138.00 | 26.5 ~ 28.5 | 22.45 | 27.33 | 19.52 | 20.11 | 23.52 | 25.42 | 38 | 165.102 | 9 EA | 10825 | 3380 | 7445 | 15260 | 35.0319 | ø 812.8x8.74t | 11 | 26.5 ~ 28.5 | matid=3, Sd= 138.0 MPa, | 51.81 | 39.11 | 40.29 | 47.13 |
| 2 | V-1110A/B | DIV. 1 | 1,3 Butane | 0.6215 | 15650 | 3.0 | 10825 | 14080 | 6.0 | 1.01325 | -19 | 68 | 10 | OK | SA516-70 | 138.00 | 26.5 ~ 26.5 | 22.45 | 22.46 | 15.61 | 18.71 | 22.88 | 25.42 | 38 | 160.064 | 9 EA | 10825 | 3380 | 7445 | 15260 | 35.0319 | ø 812.8x8.74t | 11 | 26.5 ~ 26.5 | matid=3, Sd= 138.0 MPa, | 42.02 | 31.27 | 37.47 | 45.82 |
| 3 | V-1110A/B | DIV. 2 | Propylene | 0.59 | 25200 | 1.5 | 15600 | 20266 | 8.335653 | 1.01325 | -19 | 68 | 14 | OK | SA537-CL2 | 230.00 | 35.5 ~ 35.5 | 27.55 | 27.58 | 20.62 | 26.39 | 29.84 | 34.36 | 88 | 555.967 | 14 EA | 15600 | 4800 | 10800 | 24690 | 26.9628 | ø 1066.8x15.09t | 13 | 35.5 ~ 35.5 | matid=6, Sd= 230.0 MPa, t ≤ 64t | 53.71 | 41.27 | 52.84 | 59.74 |
 S-Tank Engineering |
Spherical Tank Calculation | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : V-1110A/B자재 중량표 | Rev. No. | [AAA4] | ||||||
(1/3) Tank No. : [V-1110A/B] 자재 중량표 CALC_SPH_BODY_WEIGHT()
Design Code : Div. 1, Di = 15650 mm, DLL = 14080 mm, CA = 3 mm, SG = 0.6215, Pg = 600 kPa, Pe = 101.325 kPa
, SA516-70 matid=3, Sd= 138.0 MPa, St= 234.0 MPa,
[여기에 현장 용접 길이를 넣는다.INSERTTANKNO102]
, SA516-70 matid=3, Sd= 138.0 MPa, St= 234.0 MPa,
| Calculation Result of Required Thickness, (mm) | Used Thickness, (mm) | ||||||||||||||||||
| No. | Each Angle | Sum. Angle | Hmm | 1)tShear Theory σeq | 2.tdReq ASME CODE | 3.ttReq MAWP Site | 4.ttReq MAP Shop | 5.teReq External Pressure | tUsed thick. | PNo | SEG. Angle | Matl | tUsed thick. | Width | Height | Qty | Unit WT | Net WT | Remark |
| P | deg. | deg. | mm | mm | mm | mm | mm | mm | mm | # | deg. | mm | mm | mm | SHT | kg/sht | kg | ||
| 1 | 0.0o | 0.0o | 15650.0 | 20.02 | 24.28 | 16.90 | 20.31 | 25.42 | 26.5 | #1 | 30.0o | SA516-70 | 26.5 | 2731.4 | 8194.3 | 3 | 4,423 | 13,270 | typ=0 | 10.0o | 10.0o | 15531.1 | 20.02 | 24.28 | 16.92 | 20.34 | 25.42 | 26.5 | typ=4 | 20.0o | 30.0o | 14601.6 | 20.02 | 24.28 | 17.11 | 20.53 | 25.42 | 26.5 | typ=4 |
| 2 | 20.0o | 50.0o | 12854.8 | 20.23 | 24.55 | 17.47 | 20.88 | 25.42 | 26.5 | #2 | 20.0o | SA516-70 | 26.5 | 2731.4 | 8677.2 | 4 | 3,830 | 15,319 | typ=3 |
| 3 | 16.0o | 66.0o | 11007.7 | 20.56 | 24.95 | 17.85 | 21.26 | 25.42 | 26.5 | #3 | 16.0o | SA516-70 | 26.5 | 2495.3 | 8194.3 | 6 | 3,149 | 18,892 | typ=3 |
| 4 | 24.0o | 90.0o | 7825.0 | 21.32 | 25.64 | 18.50 | 21.91 | 25.42 | 27.5 | #4 | 64.0o | SA516-70 | 27.5 | 2731.4 | 8840.6 | 18 | 4,843 | 87,165 | typ=1 |
| 40.0o | 130.0o | 2795.2 | 21.97 | 26.73 | 19.54 | 22.95 | 25.42 | 27.5 | typ=4 | ||||||||||
| 5 | 20.0o | 150.0o | 1048.4 | 22.27 | 27.10 | 19.89 | 23.31 | 25.42 | 28.0 | #5 | 20.0o | SA516-70 | 28.0 | 2731.4 | 8477.2 | 4 | 4,046 | 16,186 | typ=3 |
| 6 | 20.0o | 170.0o | 118.9 | 22.43 | 27.30 | 20.08 | 23.50 | 25.42 | 28.5 | #6 | 30.0o | SA516-70 | 28.5 | 2731.4 | 8194.3 | 3 | 4,757 | 14,271 | typ=2 | 10.0o | 180.0o | 0.0 | 22.45 | 27.33 | 20.11 | 23.52 | 25.42 | 28.5 | typ=4 |
| Sub-Total | 38 | Sht | 165,102 | kg | |||||||||||||||
 S-Tank Engineering |
Spherical Tank Calculation | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : V-1110A/B자재 중량표 | Rev. No. | [AAA4] | ||||||
(2/3) Tank No. : [V-1110A/B] 자재 중량표 CALC_SPH_BODY_WEIGHT()
Design Code : Div. 1, Di = 15650 mm, DLL = 14080 mm, CA = 3 mm, SG = 0.6215, Pg = 600 kPa, Pe = 101.325 kPa
, SA516-70 matid=3, Sd= 138.0 MPa, St= 234.0 MPa,
[여기에 현장 용접 길이를 넣는다.INSERTTANKNO103]
, SA516-70 matid=3, Sd= 138.0 MPa, St= 234.0 MPa,
| Calculation Result of Required Thickness, (mm) | Used Thickness, (mm) | ||||||||||||||||||
| No. | Each Angle | Sum. Angle | Hmm | 1)tShear Theory σeq | 2.tdReq ASME CODE | 3.ttReq MAWP Site | 4.ttReq MAP Shop | 5.teReq External Pressure | tUsed thick. | PNo | SEG. Angle | Matl | tUsed thick. | Width | Height | Qty | Unit WT | Net WT | Remark |
| P | deg. | deg. | mm | mm | mm | mm | mm | mm | mm | # | deg. | mm | mm | mm | SHT | kg/sht | kg | ||
| 1 | 0.0o | 0.0o | 15650.0 | 20.02 | 20.02 | 16.14 | 20.31 | 25.42 | 26.5 | #1 | 30.0o | SA516-70 | 26.5 | 2731.4 | 8194.3 | 3 | 4,423 | 13,270 | typ=0 | 10.0o | 10.0o | 15531.1 | 20.02 | 20.02 | 16.16 | 20.33 | 25.42 | 26.5 | typ=4 | 20.0o | 30.0o | 14601.6 | 20.02 | 20.02 | 16.31 | 20.48 | 25.42 | 26.5 | typ=4 |
| 2 | 20.0o | 50.0o | 12854.8 | 20.23 | 20.24 | 16.60 | 20.77 | 25.42 | 26.5 | #2 | 20.0o | SA516-70 | 26.5 | 2731.4 | 8677.2 | 4 | 3,830 | 15,319 | typ=3 |
| 3 | 16.0o | 66.0o | 11007.7 | 20.56 | 20.56 | 16.90 | 21.07 | 25.42 | 26.5 | #3 | 16.0o | SA516-70 | 26.5 | 2495.3 | 8194.3 | 6 | 3,149 | 18,892 | typ=3 |
| 4 | 24.0o | 90.0o | 7825.0 | 21.31 | 21.11 | 17.42 | 21.59 | 25.42 | 26.5 | #4 | 64.0o | SA516-70 | 26.5 | 2731.4 | 8840.6 | 18 | 4,666 | 83,996 | typ=1 |
| 40.0o | 130.0o | 2795.2 | 21.97 | 21.98 | 18.25 | 22.42 | 25.42 | 26.5 | typ=4 | ||||||||||
| 5 | 20.0o | 150.0o | 1048.4 | 22.27 | 22.28 | 18.53 | 22.70 | 25.42 | 26.5 | #5 | 20.0o | SA516-70 | 26.5 | 2731.4 | 8477.2 | 4 | 3,830 | 15,319 | typ=3 |
| 6 | 20.0o | 170.0o | 118.9 | 22.43 | 22.44 | 18.69 | 22.86 | 25.42 | 26.5 | #6 | 30.0o | SA516-70 | 26.5 | 2731.4 | 8194.3 | 3 | 4,423 | 13,270 | typ=2 | 10.0o | 180.0o | 0.0 | 22.45 | 22.46 | 18.71 | 22.88 | 25.42 | 26.5 | typ=4 |
| Sub-Total | 38 | Sht | 160,064 | kg | |||||||||||||||
 S-Tank Engineering |
Spherical Tank Calculation | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : V-1110A/B자재 중량표 | Rev. No. | [AAA4] | ||||||
(3/3) Tank No. : [V-1110A/B] 자재 중량표 CALC_SPH_BODY_WEIGHT()
Design Code : Div. 2, Di = 25200 mm, DLL = 20266 mm, CA = 1.5 mm, SG = 0.59, Pg = 833.565 kPa, Pe = 101.325 kPa
, SA537-CL2 matid=6, Sd= 230.0 MPa, St= 394.25 MPa, Thick Limit : t ≤ 64t
[여기에 현장 용접 길이를 넣는다.INSERTTANKNO104]
, SA537-CL2 matid=6, Sd= 230.0 MPa, St= 394.25 MPa, Thick Limit : t ≤ 64t
| Calculation Result of Required Thickness, (mm) | Used Thickness, (mm) | ||||||||||||||||||
| No. | Each Angle | Sum. Angle | Hmm | 1)tShear Theory σeq | 2.tdReq ASME CODE | 3.ttReq MAWP Site | 4.ttReq MAP Shop | 5.teReq External Pressure | tUsed thick. | PNo | SEG. Angle | Matl | tUsed thick. | Width | Height | Qty | Unit WT | Net WT | Remark |
| P | deg. | deg. | mm | mm | mm | mm | mm | mm | mm | # | deg. | mm | mm | mm | SHT | kg/sht | kg | ||
| 1 | 0.0o | 0.0o | 25200.0 | 24.34 | 24.36 | 22.44 | 25.88 | 34.36 | 35.5 | #1 | 19.2o | SA537-CL2 | 35.5 | 2814.9 | 8444.6 | 3 | 6,293 | 18,879 | typ=0 | 6.4o | 6.4o | 25121.5 | 24.34 | 24.36 | 22.45 | 25.89 | 34.36 | 35.5 | typ=4 | 12.8o | 19.2o | 24499.1 | 24.34 | 24.36 | 22.55 | 25.99 | 34.36 | 35.5 | typ=4 |
| 2 | 12.8o | 32.0o | 23285.4 | 24.34 | 24.36 | 22.74 | 26.18 | 34.36 | 35.5 | #2 | 12.8o | SA537-CL2 | 35.5 | 2814.9 | 9642.7 | 4 | 5,840 | 23,361 | typ=3 |
| 3 | 9.5o | 41.5o | 22036.8 | 24.34 | 24.36 | 22.93 | 26.37 | 34.36 | 35.5 | #3 | 9.5o | SA537-CL2 | 35.5 | 1873.5 | 8796.5 | 9 | 3,061 | 27,546 | typ=3 |
| 4 | 45.5o | 87.0o | 13259.4 | 25.50 | 25.47 | 24.31 | 27.75 | 34.36 | 35.5 | #4 | 45.5o | SA537-CL2 | 35.5 | 2823.6 | 10050.0 | 28 | 6,916 | 193,649 | typ=3 |
| 5 | 3.0o | 90.0o | 12600.0 | 25.54 | 25.58 | 24.42 | 27.86 | 34.36 | 35.5 | #5 | 51.5o | SA537-CL2 | 35.5 | 2827.4 | 11425.4 | 28 | 7,955 | 222,746 | typ=1 |
| 48.5o | 138.5o | 3163.2 | 27.05 | 27.07 | 25.90 | 29.34 | 34.36 | 35.5 | typ=4 | ||||||||||
| 6 | 9.5o | 148.0o | 1914.6 | 27.25 | 27.27 | 26.09 | 29.54 | 34.36 | 35.5 | #6 | 9.5o | SA537-CL2 | 35.5 | 1873.5 | 8796.5 | 9 | 3,061 | 27,546 | typ=3 |
| 7 | 12.8o | 160.8o | 700.9 | 27.44 | 27.46 | 26.28 | 29.73 | 34.36 | 35.5 | #7 | 12.8o | SA537-CL2 | 35.5 | 2814.9 | 9442.7 | 4 | 5,840 | 23,361 | typ=3 |
| 8 | 12.8o | 173.6o | 78.5 | 27.54 | 27.56 | 26.38 | 29.82 | 34.36 | 35.5 | #8 | 19.2o | SA537-CL2 | 35.5 | 2814.9 | 8444.6 | 3 | 6,293 | 18,879 | typ=2 | 6.4o | 180.0o | 0.0 | 27.55 | 27.58 | 26.39 | 29.84 | 34.36 | 35.5 | typ=4 |
| Sub-Total | 88 | Sht | 555,967 | kg | |||||||||||||||
CalcRpt[i][0]=[null
 S-Tank Engineering |
AAA Spherical Tank Calculation [1 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 0. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 1, Di = 15650 mm, CA = 3 mm, SG = 0.6215, Pg= 6.0 kg/cm2(=600 kPa), Pe= 1.01325 kg/cm2(=101.325 kPa), 수압테스트압력 GsetMAWP=861.3 kPa
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
1. Design (Operating) Condition
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
1. Design (Operating) Condition
| Segment | Each Angle | Angle α | H | Hs | Ps | Pg | P =Ps+Pg | tShear | tdReq | tUsed | Forming Margin 0.7+α | Pmax MAWP | Pmax MAP | Min.MAWP 찾기 | MinMAP 찾기 | LSR=Sa/S | ||
| No. | deg. | deg. | mm | mmH2O | kPa | kPa | kPa | mm | mm | mm | mm | MPa | MPa | MPa | MPa | LSR | ||
| 0 | 0o | 15656.0 | 0 | 0 | 600.0 | 600.0 | 20.02 | 24.28 | 26.5 | 0.7+0.38 | 0.6625 | 0.7473 | 1.0 | σeq = 104.373 | 1 / 11 | |||
| P1 | 10.0o | 10.0o | 15537.1 | 0 | 0 | 600.0 | 20.02 | 24.28 | 26.5 | 0.7+0.38 | 0.6625 | 0.7473 | 1.0 | σeq = 104.373 | 2 / 11 | |||
| P2 | 20.0o | 30.0o | 14607.2 | 0 | 0 | 600.0 | 20.02 | 24.28 | 26.5 | 0.7+0.38 | 0.6625 | 0.7473 | 1.0 | σeq = 104.373 | 3 / 11 | |||
| P3 | 20.0o | 50.0o | 12859.7 | 1223.3 | 7.5 | 607.5 | 20.23 | 24.55 | 26.5 | 0.7+0.38 | 0.6550 | 0.7473 | 1.0 | σeq = 105.686 | 4 / 11 | |||
| P4 | 16.0o | 66.0o | 11011.9 | 3071.1 | 18.7 | 618.7 | 20.56 | 24.95 | 26.5 | 0.7+0.38 | 0.6438 | 0.7473 | 1.0 | σeq = 105.37 | 5 / 11 | |||
| P5 | 24.0o | 90.0o | 7828.0 | 6255.0 | 38.1 | 638.1 | 21.32 | 25.64 | 27.5 | 0.7+0.16 | 0.6244 | 0.7473 | 1.0 | σeq = 129.645 | 6 / 11 | |||
| 40.0o | 130.0o | 2796.3 | 11286.7 | 68.8 | 668.8 | 21.97 | 26.73 | 27.5 | 0.7+0.07 | 0.6218 | 0.7754 | 1.0 | σeq = 106.873 | 8 / 11 | ||||
| P6 | 20.0o | 150.0o | 1048.8 | 13034.2 | 79.4 | 679.4 | 22.27 | 27.10 | 28.0 | 0.7+0.20 | 0.6253 | 0.7895 | 1.0 | σeq = 106.377 | 9 / 11 | |||
| P7 | 20.0o | 170.0o | 118.9 | 13964.1 | 85.1 | 685.1 | 22.43 | 27.30 | 28.5 | 0.7+0.50 | 0.6337 | 0.8036 | 1.0 | σeq = 105.157 | 10 / 11 | |||
| P8 | 10.0o | 180.0o | 0 | 14083.0 | 85.8 | 685.8 | 22.45 | 27.33 | 28.5 | 0.7+0.47 | 0.6330 | 0.8036 | 0.6218 | 0.7473 | 1.0 | σeq = 105.269 | 11 / 11 |
A) Operating :
| ||||||||
 |
| Test Case | escription | Formula | symbol | Min Value | Unit | Hydrostatic Test Condition | Selected |
| 1 | Max. Allowable Working Pressue | MAWP = (D.P) = Pg | MAWP = | 0.6000 | MPa | At Site (Hot & Corroded) | Selected |
| 2 | Max. Allowable Working Pressue | MAWP = CalcMAWP(Each Shell) | MAWP = | 0.6218 | MPa | At Site (Hot & Corroded) | N/A |
| 3 | Max. Allowable Pressue | MAP = CalcMAP(Each Shell) | MAP = | 0.7473 | MPa | At Shop ( New & Cold ) | N/A |
 S-Tank Engineering |
AAA Spherical Tank Calculation [1 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 0. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 1, Di = 15650 mm, CA = 3 mm, SG = 0.6215, Pg= 6.0 kg/cm2(=600 kPa), Pe= 1.01325 kg/cm2(=101.325 kPa), 수압테스트압력 GsetMAWP=808.3 kPa
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
2. Hydrostatic-Test Condition (at Site) MAWP : Hot-Corroded
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
2. Hydrostatic-Test Condition (at Site) MAWP : Hot-Corroded
| Segment | Each Angle | Angle α | H | Hs | Ps | Pset (Test Gage Pressure) | P =Ps+Pset | 1)ttReq Pg (Basis) | 2)ttReq MAWP | 3)ttReq MAP 공장수압 시에만사용 | tUsed | Pmax MAWP | Pmax MAP | ||
| No. | deg. | deg. | mm | mmH2O | kPa | kPa | kPa | mm | mm | mm | mm | MPa | MPa | ||
| 0 | 0o | 15650.0 | 0 | 0 | 808.3 | 808.3 | 16.31 | 16.90 | 20.31 | 26.5 | 0.6625 | 0.7473 | σeq = 173.889 | 1 / 11 | |
| P1 | 10.0o | 10.0o | 15531.1 | 118.9 | 1.2 | 809.5 | 16.33 | 16.92 | 20.34 | 26.5 | 0.6625 | 0.7473 | σeq = 174.227 | 2 / 11 | |
| P2 | 20.0o | 30.0o | 14601.6 | 1048.4 | 10.3 | 818.6 | 16.52 | 17.11 | 20.53 | 26.5 | 0.6625 | 0.7473 | σeq = 170.571 | 3 / 11 | |
| P3 | 20.0o | 50.0o | 12854.8 | 2795.2 | 27.4 | 835.7 | 16.88 | 17.47 | 20.88 | 26.5 | 0.6550 | 0.7473 | σeq = 175.484 | 4 / 11 | |
| P4 | 16.0o | 66.0o | 11007.7 | 4642.3 | 45.5 | 853.8 | 17.26 | 17.85 | 21.26 | 26.5 | 0.6438 | 0.7473 | σeq = 174.603 | 5 / 11 | |
| P5 | 24.0o | 90.0o | 7825.0 | 7825.0 | 76.7 | 885.0 | 17.91 | 18.50 | 21.91 | 27.5 | 0.6244 | 0.7473 | σeq = 211.908 | 6 / 11 | |
| 40.0o | 130.0o | 2795.2 | 12854.8 | 126.1 | 934.4 | 18.94 | 19.54 | 22.95 | 27.5 | 0.6218 | 0.7754 | σeq = 177.654 | 8 / 11 | ||
| P6 | 20.0o | 150.0o | 1048.4 | 14601.6 | 143.2 | 951.5 | 19.30 | 19.89 | 23.31 | 28.0 | 0.6253 | 0.7895 | σeq = 176.24 | 9 / 11 | |
| P7 | 20.0o | 170.0o | 118.9 | 15531.1 | 152.3 | 960.6 | 19.49 | 20.08 | 23.50 | 28.5 | 0.6337 | 0.8036 | σeq = 178.388 | 10 / 11 | |
| P8 | 10.0o | 180.0o | 0 | 15650.0 | 153.5 | 961.8 | 19.52 | 20.11 | 23.52 | 28.5 | 0.6330 | 0.8036 | σeq = 173.41 | 11 / 11 |
| No. | MAWP and Hydrostatic-test gauge setting pressure | symbol | Value (MPa) | Test Gage Pressure (kg/cm2) | Hydro. Test Location | ||||||||||
| CASE 1 | Design Internal Pressue (Pg = MAWP, BASIS) | MAWP = Pg = | 0.6000 | at Site | |||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.3×MWAP×LSR | Pset(MAWP) = | 0.7800 | 7.9538 | ||||||||||||
| CASE 2 | (Hot & Corroded) At Site : Max. Allowable Working Pressue | MAWP = | 0.6218 | at Site | |||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.3×MWAP×LSR | Pset(MAWP) = | 0.8083 | 8.2424 | ||||||||||||
| CASE 3 | ( New & Cold ) At Shop : Max. Allowable Pressue | MAP = | 0.7473 | at Shop | |||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.3×MAP×LSR | Pset(MAP) = | 0.9715 | 9.9065 | ||||||||||||
 S-Tank Engineering |
AAA Spherical Tank Calculation [1 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 0. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 1, Di = 15650 mm, CA = 3 mm, SG = 0.6215, Pg= 6.0 kg/cm2(=600 kPa), Pe= 1.01325 kg/cm2(=101.325 kPa), 수압테스트압력 GsetMAWP=808.3 kPa
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
3. MAWP/MAP Calculation
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
3. MAWP/MAP Calculation
| Segment | Each Angle | Angle α | H Liquid Level | Hd | Ps | Ht Test Water Level | Ht | Pst | tc = tUsed - CA | tUsed | Pmax MAWP | Pmax MAP | MEP | |
| No. | deg. | deg. | mm | mmH2O | kPa | mm | H2O | kPa | mm | mm | MPa | MPa | kPa | |
| 0 | 0o | 15656.0 | 0 | 0 | 15650.0 | 0 | 0 | 23.50 | 26.5 | 0.6625 | 0.7473 | 111.3584 | 1 / 11 | |
| P1 | 10.0o | 10.0o | 15537.1 | 0 | 0 | 15531.1 | 118.9 | 1.2 | 23.50 | 26.5 | 0.6625 | 0.7473 | 111.3584 | 2 / 11 |
| P2 | 20.0o | 30.0o | 14607.2 | 0 | 0 | 14601.6 | 1048.4 | 10.3 | 23.50 | 26.5 | 0.6625 | 0.7473 | 111.3584 | 3 / 11 |
| P3 | 20.0o | 50.0o | 12859.7 | 1223.3 | 7.5 | 12854.8 | 2795.2 | 27.4 | 23.50 | 26.5 | 0.6550 | 0.7473 | 111.3584 | 4 / 11 |
| P4 | 16.0o | 66.0o | 11011.9 | 3071.1 | 18.7 | 11007.7 | 4642.3 | 45.5 | 23.50 | 26.5 | 0.6438 | 0.7473 | 111.3584 | 5 / 11 |
| P5 | 24.0o | 90.0o | 7828.0 | 6255.0 | 38.1 | 7825.0 | 7825.0 | 76.7 | 23.50 | 26.5 | 0.6244 | 0.7473 | 111.3584 | 6 / 11 |
| 40.0o | 130.0o | 2796.3 | 11286.7 | 68.8 | 2795.2 | 12854.8 | 126.1 | 24.50 | 27.5 | 0.6218 | 0.7754 | 121.0107 | 8 / 11 | |
| P6 | 20.0o | 150.0o | 1048.8 | 13034.2 | 79.4 | 1048.4 | 14601.6 | 143.2 | 25.00 | 28.0 | 0.6253 | 0.7895 | 125.9863 | 9 / 11 |
| P7 | 20.0o | 170.0o | 118.9 | 13964.1 | 85.1 | 118.9 | 15531.1 | 152.3 | 25.50 | 28.5 | 0.6337 | 0.8036 | 131.0615 | 10 / 11 |
| P8 | 10.0o | 180.0o | 0 | 14083.0 | 85.8 | 0 | 15650.0 | 153.5 | 25.50 | 28.5 | 0.6330 | 0.8036 | 131.0615 | 11 / 11 |
| No. | MAWP and Hydrostatic-test gauge setting pressure | symbol | Value (MPa) | Test Gage Pressure (kg/cm2) | Hydro. Test Location | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CASE 1 | Design Internal Pressue (Pg = MAWP, BASIS) | MAWP = Pg = | 0.6000 | at Site | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.3×MWAP×LSR | Pset(MAWP) = | 0.7800 | 7.9538 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CASE 2 | (Hot & Corroded) At Site : Max. Allowable Working Pressue | MAWP = | 0.6218 | at Site | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.3×MWAP×LSR | Pset(MAWP) = | 0.8083 | 8.2424 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CASE 3 | ( New & Cold ) At Shop : Max. Allowable Pressue | MAP = | 0.7473 | at Shop | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.3×MAP×LSR | Pset(MAP) = | 0.9715 | 9.9065 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| No. | MAEP and performance in vacuum | symbol | Value kPa | Value kg/cm2 | Material Chart No. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | Design External Pressure | Pe = | 101.3250 | SA516-70 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Maximum. Allowable External Pressure | MAEP = | 111.3584 | 1.1355 | CS-2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pe < MAEP, OK | Pe < MAEP | OK | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This tank is safe in full vacuum(1 atm = 101.325 kPa) condition. Full Vacuum(1 atm = 101.325 kPa) < MAEP(MinMAEP=111.3584 kPa) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 S-Tank Engineering |
AAA Spherical Tank Calculation [1 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 0. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 1, Di = 15650 mm, CA = 3 mm, SG = 0.6215, Pg= 6.0 kg/cm2(=600 kPa), Pe= 1.01325 kg/cm2(=101.325 kPa), 수압테스트압력 GsetMAWP=808.3 kPa
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
4. Summary of Shell Thickness
], CalcRpt[i][1]=[Spherical tank, / External Pressure calc Result !! Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
4. Summary of Shell Thickness
| Segment | Each Angle | Angle α | 1.tdReq σeq | 2.tdReq ASME CODE | 3.ttReq MAWP Site | 4.ttReq MAP Shop | 5.teReq External Pressure | tUsed 결정 두께 | Forming Margin +0.7 mm | PNo | SEG. Angle | tUsed thick. | Width | Height | Qty | Unit WT | Net WT | |
| No. | deg. | deg. | mm | mm | mm | mm | mm | mm | mm | # | deg. | mm | mm | mm | SHT | kg/sht | kg | |
| 0 | 0o | 20.02 | 24.3 | 16.90 | 20.31 | 25.42 | 26.5 | 0.7+0.38 | #1 | 30.0 | 26.5 | 2731.4 | 8194.3 | 3 | 4,423 | 13,270 | 1 / 11 | |
| P1 | 10.0o | 10.0o | 20.02 | 24.3 | 16.92 | 20.34 | 25.42 | 26.5 | 0.7+0.38 | 2 / 11 | ||||||||
| P2 | 20.0o | 30.0o | 20.02 | 24.3 | 17.11 | 20.53 | 25.42 | 26.5 | 0.7+0.38 | 3 / 11 | ||||||||
| P3 | 20.0o | 50.0o | 20.23 | 24.6 | 17.47 | 20.88 | 25.42 | 26.5 | 0.7+0.38 | #2 | 20.0 | 26.5 | 2731.4 | 8677.2 | 4 | 3,830 | 15,319 | 4 / 11 |
| P4 | 16.0o | 66.0o | 20.56 | 25.0 | 17.85 | 21.26 | 25.42 | 26.5 | 0.7+0.38 | #3 | 16.0 | 26.5 | 2495.3 | 8194.3 | 6 | 3,149 | 18,892 | 5 / 11 |
| P5 | 24.0o | 90.0o | 21.32 | 25.6 | 18.50 | 21.91 | 25.42 | 27.5 | 0.7+0.16 | #4 | 64.0 | 27.5 | 2731.4 | 8840.6 | 18 | 4,843 | 87,165 | 6 / 11 |
| 40.0o | 130.0o | 21.97 | 26.7 | 19.54 | 22.95 | 25.42 | 27.5 | 0.7+0.07 | 8 / 11 | |||||||||
| P6 | 20.0o | 150.0o | 22.27 | 27.1 | 19.89 | 23.31 | 25.42 | 28.0 | 0.7+0.20 | #5 | 20.0 | 28.0 | 2731.4 | 8477.2 | 4 | 4,046 | 16,186 | 9 / 11 |
| P7 | 20.0o | 170.0o | 22.43 | 27.3 | 20.08 | 23.50 | 25.42 | 28.5 | 0.7+0.50 | #6 | 30.0 | 28.5 | 2731.4 | 8194.3 | 3 | 4,757 | 14,271 | 10 / 11 |
| P8 | 10.0o | 180.0o | 22.45 | 27.3 | 20.11 | 23.52 | 25.42 | 28.5 | 0.7+0.47 | 11 / 11 |
DivNo = 1, teReq = 25.42 mm; Pe :101.33 kPa ≤ Pa = 101.38 kPa = Factor_B / (Ro/tc)*1000 ; Factor_A=0.0625*tc/Rc = 0.0003570; Factor_B = 35.499 MPa
 S-Tank Engineering |
Spherical Tank Calculation [1 / ??? ] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : AAA3 | Rev. No. | [AAA4] | ||||||
1.1 At Design(Operating) Condition
D=15650 (cm), Sd=138 MPa, Pg=0.6 (MPa), HT_UPPCOL = 33700.0 (mm), deg_22 = 22.0 (deg), cos11 = 0.9816272 (rad)
Membrane Stres(By Roark Formula) Nθ=266.671 (N-mm), Nφ=31.757 (N-mm)
| No | Description | Symbol | Value | SI Unit | Value | Metric Unit | ||||
| 1 | Design Data : | |||||||||
| 2 | D = Tank In-Diameter | D = | 15650 | mm | 1565.0 | cm | ||||
| 3 | R = Inside Radius in Corroded Condition | R = | 7828 | mm | 782.8 | cm | ||||
| 4 | L = Design Liquid level | L = | 14080 | mm | 1408.0 | cm | ||||
| 5 | CA = Corrosion Allowance | CA = | 3.0 | mm | 0.3 | cm | ||||
| 6 | Wt = Total Weight at Operating Condition | Wt = | 13,575,710 | N | 1384337.2 | Kg | ||||
| 7 | S = Allowable Stress for the Design Condition SA516-70, Sd = 138MPa | S = | 138.0 | MPa | 1407.208 | Kg/cm² | ||||
| 8 | P = Design internal GAS Pressure | P = | 0.6 | MPa | 6.118 | Kg/cm² | ||||
| 9 | SG = Design Specific Gravity | SG = | 0.622 | 0.6215 | ||||||
| 10 | γ = Liquid Density | γ = | 6.094833E-6 | N/mm³ | 621.5 | Kg/m³ | ||||
| 11 | d = Outsdie diameter of Column | d = | 812.8 | mm | 81.28 | cm | ||||
| 12 | N = Number of Support Column | N = | 9.0 | columns | 9 | columns | ||||
| 13 | Δ = Angle of equator line to column top point | Δ = | 0.0 | degree | 0 | radians | ||||
| 14 | φ = Angle of upper column from top to base | φ = | 25.51015 | degree | 0.44524 | radians | ||||
| 15 | β = Angle of Liquid Level, β=Acos[(L+CA-R)/R] | β = | 36.96007 | degree | 0.64507 | radians | ||||
| 16 | C1 = cos(Δ + φ/2) / cos(11) | C1 = | 0.9935776 | 0.9935776 | ||||||
| 17 | C2 = Factor | C2 = | 1.0000000 | 1.0000000 | ||||||
| 18 | C3 = { sin(Δ+φ ) - sin(Δ) } / sin(22) | C3 = | 1.1496619 | 1.1496619 | ||||||
| 19 | C4 = sin(Δ+φ ) + sin(Δ) | C4 = | 0.4306709 | 0.4306709 | ||||||
| 20 | C5 = 22 / φ | C5 = | 0.8624020 | 0.8624020 | ||||||
| 21 | C6 = sin(Δ+φ) + sin(Δ) | C6 = | 0.4306709 | 0.4306709 | ||||||
| 22 | Calculation Result : | |||||||||
| 23 | PM = P×R/2 | PM = | 2348.4 | N-mm | 23.947 | Kg-cm | ||||
| 24 | Nθ = γR²/6 × [6×cosβ-6×cosθ-3×cosβ×cos²θ+4×cos³θ-cos³β)/(1-cos²θ)] | Nθ = | 266.671 | N-mm | 2.719 | Kg-cm | ||||
| 25 | Nφ = γR²/6 × [( cos³β - 3×cos²θ×cosβ + 2×cos³θ) / ( 1-cos²θ)] | Nφ = | 31.757 | N-mm | 0.324 | Kg-cm | ||||
| 26 | ΣNθ = Max. Latitude Membrane Force ΣNθ = Nθ + PM + VB - HB | ΣNθ = | 2764.79 | N/mm | 2819.301 | Kg/cm | ||||
| 27 | ΣNφ = Max. Meridional Membrane Force ΣNφ = Nφ + PM - IP | ΣNφ = | 2142.12 | N/mm | 2184.354 | Kg/cm | ||||
| 28 | Equator plate thk by Internal Pressure (by ASME Rules) | tASME = | 27.33 | mm | 2.733 | cm | ||||
| 29 | t(Point A) = Min. required thickness at point at A
| tReq = | 21.32 | mm | 2.132 | cm | ||||
| 30 | Effective equivalent stress(Von-Mises), σeq < S then OK
| σeq = | 99.14 | MPa | 1010.947 | Kg/cm² | ||||
| 31 | Calculation Result : | |||||||||
| 32 | Mo = Wt R cos(11) / N x { N / (2π)- 1 / (2 x Tan(π/N) ) } | Mo = | 679,873,690 | N-mm | 6932.782×103 | Kg-cm | ||||
| 33 | ΔMo = 3 Wt R / 4π × [ 0.2616 × ( 1+0.88196.4 × C5/N) / N + 0.02804 × ( 0.88196.4 × C5/N - 1 ) / C5 ] | ΔMo = | 246,165,559 | N-mm | 2510.19×103 | Kg-cm | ||||
| 34 | Mc = Wt R cos(11) / N x { 1 / 2 × sin(π/N)) - N / (2π) ) } | Mc = | 342,021,159 | N-mm | 3487.645×103 | Kg-cm | ||||
| 35 | ΔMc = 3 Wt R / 4π × [-0.5232 × ( 1+0.88196.4 × C5/N) / N + 0.02804 × ( 1 - 0.88196.4 × C5/N ) / C5 ] | ΔMc = | 114,836,452 | N-mm | 1171.006×103 | Kg-cm | ||||
| 36 | VB : Membrance Force resulting from longitudinal bending moment VB = Mvs / Za × t | VB = | 202.422 | N/mm | 206.413 | Kg/cm | ||||
| 37 | Mvs = Mo × C1 - ΔMo × C3 | Mvs = | 392,500,102 | N-mm | 4002.387×103 | Kg-cm | ||||
| 38 | Mvm = Mc × C1 - ΔMc × C3 | Mvm = | 207,801,468 | N-mm | 2118.985×103 | Kg-cm | ||||
| 39 | Za = IH / LA × t | Za = | 55,262,047 | mm³ | 55.262×103 | cm³ | ||||
| 40 | IH = R³ × [ VI x sin( φ/2)² + HI x cos(φ/2)² ] | IH = | 3,323,586,510 | mm³ | 3323.587×103 | cm³ | ||||
| 41 | VI = φ / 2 + ( sinφ/2 × cosφ/2 ) - [ 4 x sin(Δ/2)² / φ ] | VI = | 2.4129E-5 | 2.4129E-5 | ||||||
| 42 | HI = φ / 2 - ( sinφ/2 × cosφ/2 ) | HI = | 7.28256E-3 | 7.28256E-3 | ||||||
| 43 | LA = { R×sinφ/2×sinφ/2 } / ( φ/2 ) ) | LA = | 1714.056 | mm | 171.406 | cm | ||||
| 44 | HB : Membrance Force resulting from latitude bending moment HB = Mks / Zv | HB = | 52.708 | N/mm | 53.747 | Kg/cm | ||||
| 45 | Mks = Mo x ( 18 / 4π ) × ( d / R ) × C1 × C5 × C6 | Mks = | 37,314,775 | N-mm | 380.505×103 | Kg-cm | ||||
| 46 | Mkm = Mc x ( 18 / 4π ) × ( d / R ) × C1 × C5 × C6 | Mkm = | 18,771,785 | N-mm | 191.419×103 | Kg-cm | ||||
| 47 | Zv = IV / Max(KA, KB) | Zv = | 707,956 | mm³ | 7079.563 | cm² | ||||
| 48 | IV = R³ × [ VI × cos( φ/2)² + HI × sin( φ/2)² ] | IV = | 181,292,990 | mm³ | 181.293×103 | cm³ | ||||
| 49 | KA = R × [ 1 - cosφ/2 × sinφ/2 / (φ/2) ] | KA = | 256.079 | mm | 25.608 | cm | ||||
| 50 | KB = R × [ cosφ/2 × sinφ/2 / (φ/2) - cosφ ] | KB = | 507.08 | mm | 50.708 | cm | ||||
| 51 | IP : Membrance Force resulting from shear stress IP = 9×Wt / ( 2πN·R ) × C5 | IP = | 238.035 | N/mm | 242.728 | Kg/cm | ||||
| 52 | τxy : Shear Force, τxy = ( S' - P' ) / D' | τxy = | 164.257 | N/mm | 167.496 | Kg/cm | ||||
| 53 | S' = Wt/N×[ 1 - ( 18/(4π)·d/R·C5·{cos(Δ) + cos(φ)} ) ] | S' = | 1,140,324 | N | 116280.7 | Kg | ||||
| 54 | P' = d/R×Wt×[ 3/(4π)×{cos(Δ) - cos(Δ+φ) } ] | P' = | 32807.354 | N | 3345.4 | Kg | ||||
| 55 | D' = 2×R×[sin(Δ+φ) - sinΔ](용접접촉부 길이) | D' = | 6742.584 | mm | 674.258 | cm |
piDeg=[25.510146359306425] piRad=[0.4452360466355415] SPH_IHI_EQPL_SHEAR.jsp SPH_IHI_EQPL_SHEAR()
1.1 At Design(Operating) Condition Equator Plate(A Point at 90 deg) Stress :
D=15650 (cm), Sd=138 MPa, Pg=0.6 (MPa), HT_UPPCOL = 33700.0 (mm), deg_22 = 22.0 (deg), cos11 = 0.9816272 (rad)
| 각도 Data | 최대 변형에너지 Theory 이론에 의한 검증 by, Effective equivalent Stress(Von-Mises) | ASME DESIN RULE 에 의한 두께 와 최대변형에너지 Theory(Von-Mises Stress) 에 의한 두께 계산의 평가 | Nθ, Nφ 계산상수 Coeif. | ||||||||||||||||||||||||
| Segment Angle | Hmm | Hd Liquid Depth | Static Head Ps | Total Pressure Pt=Pg+Ps | PM = P*R/2 | Nθ | Nφ | VB | HB | IP | τxy | ΣNθ | ΣNφ | σeq | 평가 | Sd | A)Shear tReq | B)ASME tReq | C)tu= Max(A,B) | A - B 두께차이 | Design Margin (%) | Nθ coef. | Nφ coef. | Nθ coef. / 6 | Nφ coef. / 6 | ||
| No | deg. | mm | mm | MPa | MPa | N/mm | N/mm | N/mm | N/mm | MPa | < OK! | MPa | mm | mm | mm | mm | % | ||||||||||
| 0 | 15656.0 | 0 | 0 | 0.6 | 2348.4 | 2348.40 | 2348.40 | 104.37 | < OK | 138 | 20.02 | 24.28 | 25.5 | 4.26 | 24.37 | 0 | 0 | 0 | 0 | ||||||||
| P1 | 10 | 15537.1 | 0 | 0 | 0.6 | 2348.4 | 2348.40 | 2348.40 | 104.37 | < OK | 138 | 20.02 | 24.28 | 25.5 | 4.26 | 24.37 | 0 | 0 | 0 | 0 | |||||||
| P2 | 30 | 14607.2 | 0 | 0 | 0.6 | 2348.4 | 2348.40 | 2348.40 | 104.37 | < OK | 138 | 20.02 | 24.28 | 25.5 | 4.26 | 24.37 | 0 | 0 | 0 | 0 | |||||||
| P3 | 50 | 12859.7 | 1223.3 | 0.0075 | 0.6075 | 2348.4 | 52.96 | 5.40 | 2401.36 | 2353.80 | 105.69 | < OK | 138 | 20.23 | 24.55 | 25.5 | 4.32 | 23.42 | 0.851 | 0.087 | 0.142 | 0.014 | |||||
| P4 | 66 | 11011.9 | 3071.1 | 0.0187 | 0.6187 | 2348.4 | 128.01 | 18.51 | 2476.41 | 2366.91 | 105.37 | < OK | 138 | 20.56 | 24.95 | 26.0 | 4.39 | 23.64 | 2.057 | 0.297 | 0.343 | 0.05 | |||||
| P5 | 90 | 7828.0 | 6255.0 | 0.0381 | 0.6381 | 2348.4 | 266.67 | 31.76 | 202.42 | 52.71 | 238.04 | 164.26 | 2764.79 | 2142.12 | 129.64 | < OK | 138 | 21.32 | 25.64 | 22.5 | 4.32 | 6.05 | 4.284 | 0.51 | 0.714 | 0.085 | Column Attached Equator Plate |
| 130 | 2796.3 | 11286.7 | 0.0688 | 0.6688 | 2348.4 | 233.48 | 305.02 | 2581.88 | 2653.42 | 106.87 | < OK | 138 | 21.97 | 26.72 | 27.5 | 4.75 | 22.56 | 3.751 | 4.9 | 0.625 | 0.817 | ||||||
| P6 | 150 | 1048.8 | 13034.2 | 0.0794 | 0.6794 | 2348.4 | 298.13 | 323.74 | 2646.53 | 2672.14 | 106.38 | < OK | 138 | 22.27 | 27.10 | 28.0 | 4.83 | 22.92 | 4.789 | 5.201 | 0.798 | 0.867 | |||||
| P7 | 170 | 118.9 | 13964.1 | 0.0851 | 0.6851 | 2348.4 | 331.69 | 334.54 | 2680.09 | 2682.94 | 105.16 | < OK | 138 | 22.43 | 27.30 | 28.5 | 4.87 | 23.80 | 5.329 | 5.374 | 0.888 | 0.896 | |||||
| P8 | 180 | 0 | 14083.0 | 0.0858 | 0.6858 | 2348.4 | 335.95 | 335.95 | 2684.35 | 2684.35 | 105.27 | < OK | 138 | 22.45 | 27.33 | 28.5 | 4.88 | 23.72 | 5.397 | 5.397 | 0.9 | 0.9 | |||||

 S-Tank Engineering |
Spherical Tank Calculation [1 / ??? ] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : AAA3 | Rev. No. | [AAA4] | ||||||
1.2 At Hydrostatic-Test Condition
D=15650 (cm), Syt=234 MPa, MAWP=0.78 (MPa), HT_UPPCOL = 33800.0 (mm), deg_22 = 22.0 (deg), cos11 = 0.9816272 (rad)
Membrane Stres(By Roark Formula) Nθ=500.389 (N-mm), Nφ=100.078 (N-mm)
| No | Description | Symbol | Value | SI Unit | Value | Metric Unit | ||||
| 1 | Design Data : | |||||||||
| 2 | D = Tank In-Diameter | D = | 15650 | mm | 1565.0 | cm | ||||
| 3 | R = Inside Radius in Corroded Condition | R = | 7825 | mm | 782.5 | cm | ||||
| 4 | L = Hydrostatic-test Water Level | L = | 15650 | mm | 1565.0 | cm | ||||
| 5 | CA = Corrosion Allowance | CA = | 0.0 | mm | 0 | cm | ||||
| 6 | Wt = Total Weight at Operating Condition | Wt = | 20,895,976 | N | 2130796.5 | Kg | ||||
| 7 | S = Allowable Stress for the Design Condition SA516-70, Sd = 234MPa | S = | 234.0 | MPa | 2386.136 | Kg/cm² | ||||
| 8 | P = Design internal GAS Pressure | P = | 0.6 | MPa | 6.118 | Kg/cm² | ||||
| 9 | SG = Design Specific Gravity | SG = | 1.0 | 1 | ||||||
| 10 | γ = Liquid Density | γ = | 9.80665E-6 | N/mm³ | 1000.0 | Kg/m³ | ||||
| 11 | d = Outsdie diameter of Column | d = | 812.8 | mm | 81.28 | cm | ||||
| 12 | N = Number of Support Column | N = | 9.0 | columns | 9 | columns | ||||
| 13 | Δ = Angle of equator line to column top point | Δ = | 0.0 | degree | 0 | radians | ||||
| 14 | φ = Angle of upper column from top to base | φ = | 25.5913 | degree | 0.44665 | radians | ||||
| 15 | β = Angle of Liquid Level, β=Acos[(L+CA-R)/R] | β = | 0.0 | degree | 0 | radians | ||||
| 16 | C1 = cos(Δ + φ/2) / cos(11) | C1 = | 0.9934181 | 0.9934181 | ||||||
| 17 | C2 = Factor | C2 = | 1.0000000 | 1.0000000 | ||||||
| 18 | C3 = { sin(Δ+φ ) - sin(Δ) } / sin(22) | C3 = | 1.1530734 | 1.1530734 | ||||||
| 19 | C4 = sin(Δ+φ ) + sin(Δ) | C4 = | 0.4319489 | 0.4319489 | ||||||
| 20 | C5 = 22 / φ | C5 = | 0.8596670 | 0.8596670 | ||||||
| 21 | C6 = sin(Δ+φ) + sin(Δ) | C6 = | 0.4319489 | 0.4319489 | ||||||
| 22 | Calculation Result : | |||||||||
| 23 | PM = P×R/2 | PM = | 2347.5 | N-mm | 23.938 | Kg-cm | ||||
| 24 | Nθ = γR²/6 × [6×cosβ-6×cosθ-3×cosβ×cos²θ+4×cos³θ-cos³β)/(1-cos²θ)] | Nθ = | 500.389 | N-mm | 5.103 | Kg-cm | ||||
| 25 | Nφ = γR²/6 × [( cos³β - 3×cos²θ×cosβ + 2×cos³θ) / ( 1-cos²θ)] | Nφ = | 100.078 | N-mm | 1.021 | Kg-cm | ||||
| 26 | ΣNθ = Max. Latitude Membrane Force ΣNθ = Nθ + PM + VB - HB | ΣNθ = | 3077.31 | N/mm | 3137.983 | Kg/cm | ||||
| 27 | ΣNφ = Max. Meridional Membrane Force ΣNφ = Nφ + PM - IP | ΣNφ = | 2082.21 | N/mm | 2123.263 | Kg/cm | ||||
| 28 | Equator plate thk by Internal Pressure (by ASME Rules) | tASME = | 15.75 | mm | 1.575 | cm | ||||
| 29 | t(Point A) = Min. required thickness at point at A
| tReq = | 11.77 | mm | 1.177 | cm | ||||
| 30 | Effective equivalent stress(Von-Mises), σeq < S then OK
| σeq = | 162.047 | MPa | 1652.42 | Kg/cm² | ||||
| 31 | Calculation Result : | |||||||||
| 32 | Mo = Wt R cos(11) / N x { N / (2π)- 1 / (2 x Tan(π/N) ) } | Mo = | 1,046,072,706 | N-mm | 10666.973×103 | Kg-cm | ||||
| 33 | ΔMo = 3 Wt R / 4π × [ 0.2616 × ( 1+0.88196.4 × C5/N) / N + 0.02804 × ( 0.88196.4 × C5/N - 1 ) / C5 ] | ΔMo = | 377,464,366 | N-mm | 3849.065×103 | Kg-cm | ||||
| 34 | Mc = Wt R cos(11) / N x { 1 / 2 × sin(π/N)) - N / (2π) ) } | Mc = | 526,243,337 | N-mm | 5366.189×103 | Kg-cm | ||||
| 35 | ΔMc = 3 Wt R / 4π × [-0.5232 × ( 1+0.88196.4 × C5/N) / N + 0.02804 × ( 1 - 0.88196.4 × C5/N ) / C5 ] | ΔMc = | 176,162,442 | N-mm | 1796.357×103 | Kg-cm | ||||
| 36 | VB : Membrance Force resulting from longitudinal bending moment VB = Mvs / Za × t | VB = | 309.819 | N/mm | 315.927 | Kg/cm | ||||
| 37 | Mvs = Mo × C1 - ΔMo × C3 | Mvs = | 603,943,405 | N-mm | 6158.509×103 | Kg-cm | ||||
| 38 | Mvm = Mc × C1 - ΔMc × C3 | Mvm = | 319,651,412 | N-mm | 3259.537×103 | Kg-cm | ||||
| 39 | Za = IH / LA × t | Za = | 39,961,510 | mm³ | 39.962×103 | cm³ | ||||
| 40 | IH = R³ × [ VI x sin( φ/2)² + HI x cos(φ/2)² ] | IH = | 3,350,271,797 | mm³ | 3350.272×103 | cm³ | ||||
| 41 | VI = φ / 2 + ( sinφ/2 × cosφ/2 ) - [ 4 x sin(Δ/2)² / φ ] | VI = | 2.4514E-5 | 2.4514E-5 | ||||||
| 42 | HI = φ / 2 - ( sinφ/2 × cosφ/2 ) | HI = | 7.351823E-3 | 7.351823E-3 | ||||||
| 43 | LA = { R×sinφ/2×sinφ/2 } / ( φ/2 ) ) | LA = | 1718.668 | mm | 171.867 | cm | ||||
| 44 | HB : Membrance Force resulting from latitude bending moment HB = Mks / Zv | HB = | 80.4 | N/mm | 81.985 | Kg/cm | ||||
| 45 | Mks = Mo x ( 18 / 4π ) × ( d / R ) × C1 × C5 × C6 | Mks = | 57,414,094 | N-mm | 585.461×103 | Kg-cm | ||||
| 46 | Mkm = Mc x ( 18 / 4π ) × ( d / R ) × C1 × C5 × C6 | Mkm = | 28,883,063 | N-mm | 294.525×103 | Kg-cm | ||||
| 47 | Zv = IV / Max(KA, KB) | Zv = | 714,103 | mm³ | 7141.03 | cm² | ||||
| 48 | IV = R³ × [ VI × cos( φ/2)² + HI × sin( φ/2)² ] | IV = | 183,950,286 | mm³ | 183.95×103 | cm³ | ||||
| 49 | KA = R × [ 1 - cosφ/2 × sinφ/2 / (φ/2) ] | KA = | 257.596 | mm | 25.76 | cm | ||||
| 50 | KB = R × [ cosφ/2 × sinφ/2 / (φ/2) - cosφ ] | KB = | 510.051 | mm | 51.005 | cm | ||||
| 51 | IP : Membrance Force resulting from shear stress IP = 9×Wt / ( 2πN·R ) × C5 | IP = | 365.366 | N/mm | 372.57 | Kg/cm | ||||
| 52 | τxy : Shear Force, τxy = ( S' - P' ) / D' | τxy = | 252.387 | N/mm | 257.363 | Kg/cm | ||||
| 53 | S' = Wt/N×[ 1 - ( 18/(4π)·d/R·C5·{cos(Δ) + cos(φ)} ) ] | S' = | 1,756,969 | N | 179160.9 | Kg | ||||
| 54 | P' = d/R×Wt×[ 3/(4π)×{cos(Δ) - cos(Δ+φ) } ] | P' = | 50833.599 | N | 5183.6 | Kg | ||||
| 55 | D' = 2×R×[sin(Δ+φ) - sinΔ](용접접촉부 길이) | D' = | 6760.0 | mm | 676.0 | cm |
piDeg=[25.59130479672834] piRad=[0.44665252858432775] SPH_IHI_EQPL_SHEAR.jsp SPH_IHI_EQPL_SHEAR()
1.2 At Hydrostatic-Test Condition Equator Plate(A Point at 90 deg) Stress :
D=15650 (cm), Syt=234 MPa, MAWP=0.78 (MPa), HT_UPPCOL = 33800.0 (mm), deg_22 = 22.0 (deg), cos11 = 0.9816272 (rad)
| 각도 Data | 최대 변형에너지 Theory 이론에 의한 검증 by, Effective equivalent Stress(Von-Mises) | ASME DESIN RULE 에 의한 두께 와 최대변형에너지 Theory(Von-Mises Stress) 에 의한 두께 계산의 평가 | Nθ, Nφ 계산상수 Coeif. | ||||||||||||||||||||||||
| Segment Angle | Hmm | Hd Liquid Depth | Static Head Ps | Total Pressure Pt=Pg+Ps | PM = P*R/2 | Nθ | Nφ | VB | HB | IP | τxy | ΣNθ | ΣNφ | σeq | 평가 | Sd | A)Shear tReq | B)ASME tReq | C)tu= Max(A,B) | A - B 두께차이 | Design Margin (%) | Nθ coef. | Nφ coef. | Nθ coef. / 6 | Nφ coef. / 6 | ||
| No | deg. | mm | mm | MPa | MPa | N/mm | N/mm | N/mm | N/mm | MPa | < OK! | MPa | mm | mm | mm | mm | % | ||||||||||
| 0 | 15650.0 | 0 | 0 | 0.6 | 2347.5 | 2347.50 | 2347.50 | 173.89 | < OK | 234 | 10.03 | 12.54 | 13.5 | 2.51 | 25.69 | 0 | 0 | 0 | 0 | ||||||||
| P1 | 10 | 15531.1 | 118.9 | 0.0012 | 0.6012 | 2347.5 | 6.85 | 2.27 | 2354.35 | 2349.77 | 174.23 | < OK | 234 | 10.05 | 12.57 | 13.5 | 2.52 | 25.54 | 0.068 | 0.023 | 0.011 | 0.004 | |||||
| P2 | 30 | 14601.6 | 1048.4 | 0.0103 | 0.6103 | 2347.5 | 60.82 | 19.63 | 2408.32 | 2367.13 | 170.57 | < OK | 234 | 10.21 | 12.76 | 14.0 | 2.55 | 27.11 | 0.608 | 0.196 | 0.101 | 0.033 | |||||
| P3 | 50 | 12854.8 | 2795.2 | 0.0274 | 0.6274 | 2347.5 | 164.76 | 49.74 | 2512.26 | 2397.24 | 175.48 | < OK | 234 | 10.50 | 13.12 | 14.0 | 2.62 | 25.01 | 1.646 | 0.497 | 0.274 | 0.083 | |||||
| P4 | 66 | 11007.7 | 4642.3 | 0.0455 | 0.6455 | 2347.5 | 279.70 | 76.54 | 2627.20 | 2424.04 | 174.60 | < OK | 234 | 10.82 | 13.50 | 14.5 | 2.68 | 25.38 | 2.795 | 0.765 | 0.466 | 0.127 | |||||
| P5 | 90 | 7825.0 | 7825.0 | 0.0767 | 0.6767 | 2347.5 | 500.39 | 100.08 | 309.82 | 80.40 | 365.37 | 252.39 | 3077.31 | 2082.21 | 211.91 | < OK | 234 | 11.77 | 14.15 | 13.0 | 2.38 | 9.44 | 5 | 1 | 0.833 | 0.167 | Column Attached Equator Plate |
| 130 | 2795.2 | 12854.8 | 0.1261 | 0.7261 | 2347.5 | 435.71 | 550.73 | 2783.21 | 2898.23 | 177.65 | < OK | 234 | 12.15 | 15.18 | 16.0 | 3.03 | 24.08 | 4.354 | 5.503 | 0.726 | 0.917 | ||||||
| P6 | 150 | 1048.4 | 14601.6 | 0.1432 | 0.7432 | 2347.5 | 539.65 | 580.84 | 2887.15 | 2928.34 | 176.24 | < OK | 234 | 12.43 | 15.54 | 16.5 | 3.11 | 24.68 | 5.392 | 5.804 | 0.899 | 0.967 | |||||
| P7 | 170 | 118.9 | 15531.1 | 0.1523 | 0.7523 | 2347.5 | 593.62 | 598.19 | 2941.12 | 2945.69 | 178.39 | < OK | 234 | 12.58 | 15.73 | 16.5 | 3.15 | 23.77 | 5.932 | 5.977 | 0.989 | 0.996 | |||||
| P8 | 180 | 0 | 15650.0 | 0.1535 | 0.7535 | 2347.5 | 600.47 | 600.47 | 2947.97 | 2947.97 | 173.41 | < OK | 234 | 12.60 | 15.75 | 17.0 | 3.15 | 25.89 | 6 | 6 | 1 | 1 | |||||

], CalcRpt[i][2]=[SPH_IHI_SHEAR.jsp CALC_SPH_COL_BRA_ACCY_WEIGHT()
● WEIGHT SUMMARY SPH_IHI_SHEAR.jsp CALC_SPH_COL_BRA_ACCY_WEIGHT() BRACE AXIAL-FORCE DESIGN DATA
MRA(sWt[tid][20][1])= 0
MRA(sWt[tid][20][2])= 0
MRA(sWt[tid][20][3])= 38
MRA(sWt[tid][20][4])= 0
MRA(sWt[tid][20][5])= 165102.233
MRA(sWt[tid][20][6])= 0
MRA(sWt[tid][20][7])= 0
MRA(sWt[tid][20][8])= 0
MRA(sWt[tid][20][9])= 15650
MRA(sWt[tid][20][10])= 769.446
UPPER COLUMN : cbMatl[tid][0] = null
LOWER COLUMN : cbMatl[tid][1] = null
BRACE cbMatl[tid][2] = null
| 1. gCol[tid][1] = | Column Q'ty | Nc = | 9 | Columns |  |
| 2. gCol[tid][2] = | Column OD | OD = | 812.8 | mm | |
| 3. gCol[tid][3] = | Column thk | thk = | 8.74 | mm | |
| 4. gCol[tid][4] = | Tank Height | Htank = | 10825 | mm | |
| 5. gCol[tid][5] = | Upper Column Height | UCHT = | 3380 | mm | |
| 6. gCol[tid][6] = | Lower Column Height | LCHT = | 7445 | mm | |
| 7. gCol[tid][7] = | Column P.C.D | PCD = | 15260 | mm | |
| 8. gCol[tid][8] = | Brace Angle | BRang = | 35.0319 | deg. | |
| 9. gCol[tid][9] = | Brace Angle of Tank center to Brace Center | BRang_CTR = | 12.818 | deg | |
| 10. gCol[tid][10] = | Column CA | CA = | 0 | mm | |
| 11. gCol[tid][11] = | Brace OD | BR_OD = | 0 | mm | |
| 12. gCol[tid][12] = | Brace Thk | BR_Thk = | 0 | mm | |
| 13. gCol[tid][13] = | Brace CA | BR_CA = | 0 | mm |
A) TANK 제작비/자재비/도장비/외주비 부문
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 |
| No. | Description | Main Material | Thk. and Size | Unit | QTY | Net Wt kg | Gross Wt kg | 자재비 | 제작비 | No |
| 1 | SHELL PLATE | SA516-70 | t26.5 ~ 28 | SHT | 38 | 165.102 | 201.425 | 000,000 | 000,000 | 1 |
| 2 | UPPER COLUMN(PLATE) (재고확인) | null | t28, t11×2853×3380 | SHT | 9 | 8.625 | 9.488 | 000,000 | 000,000 | 2 |
| 3 | LOWER COLUMN (PIPE) | null | Ø812.8×8.74t × 7445L | PCS | 9 | 11.612 | 11.612 | 000,000 | 000,000 | 3 |
| 4 | BRACE ( PIPE, θ= 35.0319 deg.) | null | Ø0×0t × 9092L | PCS | 18 | 000,000 | 000,000 | 4 | ||
| 5 | COLUMN ACC'Y (PLATE) | A36 OR SS400 | - | LOT | 000,000 | 000,000 | 5 | |||
| 6 | BASE PLATE & ANCHOR BOLT (NO SITE PWHT = NO SLIDEING PLATE) | By SPEC. | SEE. Bellow TABLE 4) | LOT | 000,000 | 000,000 | 6 | |||
| 7 | NOZZLE & MANHOLE(DIP. PIPE) | Forging | Assumed Qty : 19 | 19 | 000,000 | 000,000 | 7 | |||
| 8 | ROOF PLATFORM & STRINGER | CLIP:SA516-70(OR CS) | PLATE & SHAPE | LOT | 000,000 | 000,000 | 8 | |||
| 9 | WATER SPRAY (Only Proposal) | By SPEC. | PIPE & ACC'Y | 15 | 000,000 | 000,000 | 9 | |||
| 10 | INTERNAL LADDER (Only Proposal) | SA516-70 | PLATE & SHAPE | LOT | 000,000 | 000,000 | 10 | |||
| 11 | INSULATION (Only Proposal) | By SPEC. | - | LOT | 000,000 | 000,000 | 11 | |||
| 12 | GRAND TOTAL | 74 | 185.339 | 222.524 | 000,000 | 000,000 | 12 |
 S-Tank Engineering |
AAA Spherical Tank Calculation [2 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 1. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 1, Di = 15650 mm, CA = 3 mm, SG = 0.6215, Pg= 6.0 kg/cm2(=600 kPa), Pe= 1.01325 kg/cm2(=101.325 kPa), 수압테스트압력 GsetMAWP=1076.5 kPa
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
1. Design (Operating) Condition
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
1. Design (Operating) Condition
| Segment | Each Angle | Angle α | H | Hs | Ps | Pg | P =Ps+Pg | tShear | tdReq | tUsed | Forming Margin 0.7+α | Pmax MAWP | Pmax MAP | Min.MAWP 찾기 | MinMAP 찾기 | LSR=Sa/S | ||
| No. | deg. | deg. | mm | mmH2O | kPa | kPa | kPa | mm | mm | mm | mm | MPa | MPa | MPa | MPa | LSR | ||
| 0 | 0o | 15656.0 | 0 | 0 | 600.0 | 600.0 | 20.02 | 20.02 | 26.5 | 0.7+0.38 | 0.8281 | 0.9341 | 1.0 | σeq = 130.467 | 1 / 11 | |||
| P1 | 10.0o | 10.0o | 15537.1 | 0 | 0 | 600.0 | 20.02 | 20.02 | 26.5 | 0.7+0.38 | 0.8281 | 0.9341 | 1.0 | σeq = 130.467 | 2 / 11 | |||
| P2 | 20.0o | 30.0o | 14607.2 | 0 | 0 | 600.0 | 20.02 | 20.02 | 26.5 | 0.7+0.38 | 0.8281 | 0.9341 | 1.0 | σeq = 130.467 | 3 / 11 | |||
| P3 | 20.0o | 50.0o | 12859.7 | 1223.3 | 7.5 | 607.5 | 20.23 | 20.24 | 26.5 | 0.7+0.38 | 0.8206 | 0.9341 | 1.0 | σeq = 132.108 | 4 / 11 | |||
| P4 | 16.0o | 66.0o | 11011.9 | 3071.1 | 18.7 | 618.7 | 20.56 | 20.56 | 26.5 | 0.7+0.38 | 0.8094 | 0.9341 | 1.0 | σeq = 131.001 | 5 / 11 | |||
| P5 | 24.0o | 90.0o | 7828.0 | 6255.0 | 38.1 | 638.1 | 21.31 | 21.11 | 26.5 | 0.7+0.38 | 0.7900 | 0.9341 | 1.0 | σeq = 129.578 | 6 / 11 | |||
| 40.0o | 130.0o | 2796.3 | 11286.7 | 68.8 | 668.8 | 21.97 | 21.98 | 26.5 | 0.7+0.38 | 0.7593 | 0.9341 | 1.0 | σeq = 130.919 | 8 / 11 | ||||
| P6 | 20.0o | 150.0o | 1048.8 | 13034.2 | 79.4 | 679.4 | 22.27 | 22.28 | 26.5 | 0.7+0.38 | 0.7487 | 0.9341 | 1.0 | σeq = 129.728 | 9 / 11 | |||
| P7 | 20.0o | 170.0o | 118.9 | 13964.1 | 85.1 | 685.1 | 22.43 | 22.44 | 26.5 | 0.7+0.38 | 0.7430 | 0.9341 | 1.0 | σeq = 130.806 | 10 / 11 | |||
| P8 | 10.0o | 180.0o | 0 | 14083.0 | 85.8 | 685.8 | 22.45 | 22.46 | 26.5 | 0.7+0.38 | 0.7423 | 0.9341 | 0.7423 | 0.9341 | 1.0 | σeq = 130.944 | 11 / 11 |
A) Operating :
| ||||||||
 |
| Test Case | escription | Formula | symbol | Min Value | Unit | Hydrostatic Test Condition | Selected |
| 1 | Max. Allowable Working Pressue | MAWP = (D.P) = Pg | MAWP = | 0.6000 | MPa | At Site (Hot & Corroded) | Selected |
| 2 | Max. Allowable Working Pressue | MAWP = CalcMAWP(Each Shell) | MAWP = | 0.7423 | MPa | At Site (Hot & Corroded) | N/A |
| 3 | Max. Allowable Pressue | MAP = CalcMAP(Each Shell) | MAP = | 0.9341 | MPa | At Shop ( New & Cold ) | N/A |
 S-Tank Engineering |
AAA Spherical Tank Calculation [2 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 1. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 1, Di = 15650 mm, CA = 3 mm, SG = 0.6215, Pg= 6.0 kg/cm2(=600 kPa), Pe= 1.01325 kg/cm2(=101.325 kPa), 수압테스트압력 GsetMAWP=965 kPa
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
2. Hydrostatic-Test Condition (at Site) MAWP : Hot-Corroded
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
2. Hydrostatic-Test Condition (at Site) MAWP : Hot-Corroded
| Segment | Each Angle | Angle α | H | Hs | Ps | Pset (Test Gage Pressure) | P =Ps+Pset | 1)ttReq Pg (Basis) | 2)ttReq MAWP | 3)ttReq MAP 공장수압 시에만사용 | tUsed | Pmax MAWP | Pmax MAP | ||
| No. | deg. | deg. | mm | mmH2O | kPa | kPa | kPa | mm | mm | mm | mm | MPa | MPa | ||
| 0 | 0o | 15650.0 | 0 | 0 | 965.0 | 965.0 | 13.05 | 16.14 | 20.31 | 26.5 | 0.8281 | 0.9341 | σeq = 213.409 | 1 / 11 | |
| P1 | 10.0o | 10.0o | 15531.1 | 118.9 | 1.2 | 966.2 | 13.07 | 16.16 | 20.33 | 26.5 | 0.8281 | 0.9341 | σeq = 213.824 | 2 / 11 | |
| P2 | 20.0o | 30.0o | 14601.6 | 1048.4 | 10.3 | 975.3 | 13.22 | 16.31 | 20.48 | 26.5 | 0.8281 | 0.9341 | σeq = 217.09 | 3 / 11 | |
| P3 | 20.0o | 50.0o | 12854.8 | 2795.2 | 27.4 | 992.4 | 13.50 | 16.60 | 20.77 | 26.5 | 0.8206 | 0.9341 | σeq = 213.632 | 4 / 11 | |
| P4 | 16.0o | 66.0o | 11007.7 | 4642.3 | 45.5 | 1010.5 | 13.81 | 16.90 | 21.07 | 26.5 | 0.8094 | 0.9341 | σeq = 210.978 | 5 / 11 | |
| P5 | 24.0o | 90.0o | 7825.0 | 7825.0 | 76.7 | 1041.7 | 14.33 | 17.42 | 21.59 | 26.5 | 0.7900 | 0.9341 | σeq = 211.763 | 6 / 11 | |
| 40.0o | 130.0o | 2795.2 | 12854.8 | 126.1 | 1091.1 | 15.15 | 18.25 | 22.42 | 26.5 | 0.7593 | 0.9341 | σeq = 218.651 | 8 / 11 | ||
| P6 | 20.0o | 150.0o | 1048.4 | 14601.6 | 143.2 | 1108.2 | 15.44 | 18.53 | 22.70 | 26.5 | 0.7487 | 0.9341 | σeq = 215.405 | 9 / 11 | |
| P7 | 20.0o | 170.0o | 118.9 | 15531.1 | 152.3 | 1117.3 | 15.59 | 18.69 | 22.86 | 26.5 | 0.7430 | 0.9341 | σeq = 218.03 | 10 / 11 | |
| P8 | 10.0o | 180.0o | 0 | 15650.0 | 153.5 | 1118.5 | 15.61 | 18.71 | 22.88 | 26.5 | 0.7423 | 0.9341 | σeq = 218.368 | 11 / 11 |
| No. | MAWP and Hydrostatic-test gauge setting pressure | symbol | Value (MPa) | Test Gage Pressure (kg/cm2) | Hydro. Test Location | ||||||||||
| CASE 1 | Design Internal Pressue (Pg = MAWP, BASIS) | MAWP = Pg = | 0.6000 | at Site | |||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.3×MWAP×LSR | Pset(MAWP) = | 0.7800 | 7.9538 | ||||||||||||
| CASE 2 | (Hot & Corroded) At Site : Max. Allowable Working Pressue | MAWP = | 0.7423 | at Site | |||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.3×MWAP×LSR | Pset(MAWP) = | 0.9650 | 9.8403 | ||||||||||||
| CASE 3 | ( New & Cold ) At Shop : Max. Allowable Pressue | MAP = | 0.9341 | at Shop | |||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.3×MAP×LSR | Pset(MAP) = | 1.2143 | 12.3824 | ||||||||||||
 S-Tank Engineering |
AAA Spherical Tank Calculation [2 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 1. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 1, Di = 15650 mm, CA = 3 mm, SG = 0.6215, Pg= 6.0 kg/cm2(=600 kPa), Pe= 1.01325 kg/cm2(=101.325 kPa), 수압테스트압력 GsetMAWP=965 kPa
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
3. MAWP/MAP Calculation
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
3. MAWP/MAP Calculation
| Segment | Each Angle | Angle α | H Liquid Level | Hd | Ps | Ht Test Water Level | Ht | Pst | tc = tUsed - CA | tUsed | Pmax MAWP | Pmax MAP | MEP | |
| No. | deg. | deg. | mm | mmH2O | kPa | mm | H2O | kPa | mm | mm | MPa | MPa | kPa | |
| 0 | 0o | 15656.0 | 0 | 0 | 15650.0 | 0 | 0 | 23.50 | 26.5 | 0.8281 | 0.9341 | 111.3584 | 1 / 11 | |
| P1 | 10.0o | 10.0o | 15537.1 | 0 | 0 | 15531.1 | 118.9 | 1.2 | 23.50 | 26.5 | 0.8281 | 0.9341 | 111.3584 | 2 / 11 |
| P2 | 20.0o | 30.0o | 14607.2 | 0 | 0 | 14601.6 | 1048.4 | 10.3 | 23.50 | 26.5 | 0.8281 | 0.9341 | 111.3584 | 3 / 11 |
| P3 | 20.0o | 50.0o | 12859.7 | 1223.3 | 7.5 | 12854.8 | 2795.2 | 27.4 | 23.50 | 26.5 | 0.8206 | 0.9341 | 111.3584 | 4 / 11 |
| P4 | 16.0o | 66.0o | 11011.9 | 3071.1 | 18.7 | 11007.7 | 4642.3 | 45.5 | 23.50 | 26.5 | 0.8094 | 0.9341 | 111.3584 | 5 / 11 |
| P5 | 24.0o | 90.0o | 7828.0 | 6255.0 | 38.1 | 7825.0 | 7825.0 | 76.7 | 23.50 | 26.5 | 0.7900 | 0.9341 | 111.3584 | 6 / 11 |
| 40.0o | 130.0o | 2796.3 | 11286.7 | 68.8 | 2795.2 | 12854.8 | 126.1 | 23.50 | 26.5 | 0.7593 | 0.9341 | 111.3584 | 8 / 11 | |
| P6 | 20.0o | 150.0o | 1048.8 | 13034.2 | 79.4 | 1048.4 | 14601.6 | 143.2 | 23.50 | 26.5 | 0.7487 | 0.9341 | 111.3584 | 9 / 11 |
| P7 | 20.0o | 170.0o | 118.9 | 13964.1 | 85.1 | 118.9 | 15531.1 | 152.3 | 23.50 | 26.5 | 0.7430 | 0.9341 | 111.3584 | 10 / 11 |
| P8 | 10.0o | 180.0o | 0 | 14083.0 | 85.8 | 0 | 15650.0 | 153.5 | 23.50 | 26.5 | 0.7423 | 0.9341 | 111.3584 | 11 / 11 |
| No. | MAWP and Hydrostatic-test gauge setting pressure | symbol | Value (MPa) | Test Gage Pressure (kg/cm2) | Hydro. Test Location | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CASE 1 | Design Internal Pressue (Pg = MAWP, BASIS) | MAWP = Pg = | 0.6000 | at Site | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.3×MWAP×LSR | Pset(MAWP) = | 0.7800 | 7.9538 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CASE 2 | (Hot & Corroded) At Site : Max. Allowable Working Pressue | MAWP = | 0.7423 | at Site | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.3×MWAP×LSR | Pset(MAWP) = | 0.9650 | 9.8403 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| CASE 3 | ( New & Cold ) At Shop : Max. Allowable Pressue | MAP = | 0.9341 | at Shop | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.3×MAP×LSR | Pset(MAP) = | 1.2143 | 12.3824 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| No. | MAEP and performance in vacuum | symbol | Value kPa | Value kg/cm2 | Material Chart No. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | Design External Pressure | Pe = | 101.3250 | SA516-70 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Maximum. Allowable External Pressure | MAEP = | 111.3584 | 1.1355 | CS-2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pe < MAEP, OK | Pe < MAEP | OK | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This tank is safe in full vacuum(1 atm = 101.325 kPa) condition. Full Vacuum(1 atm = 101.325 kPa) < MAEP(MinMAEP=111.3584 kPa) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 S-Tank Engineering |
AAA Spherical Tank Calculation [2 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 1. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 1, Di = 15650 mm, CA = 3 mm, SG = 0.6215, Pg= 6.0 kg/cm2(=600 kPa), Pe= 1.01325 kg/cm2(=101.325 kPa), 수압테스트압력 GsetMAWP=965 kPa
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
4. Summary of Shell Thickness
], CalcRpt[i][1]=[Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
4. Summary of Shell Thickness
| Segment | Each Angle | Angle α | 1.tdReq σeq | 2.tdReq ASME CODE | 3.ttReq MAWP Site | 4.ttReq MAP Shop | 5.teReq External Pressure | tUsed 결정 두께 | Forming Margin +0.7 mm | PNo | SEG. Angle | tUsed thick. | Width | Height | Qty | Unit WT | Net WT | |
| No. | deg. | deg. | mm | mm | mm | mm | mm | mm | mm | # | deg. | mm | mm | mm | SHT | kg/sht | kg | |
| 0 | 0o | 20.02 | 20.0 | 16.14 | 20.31 | 25.42 | 26.5 | 0.7+0.38 | #1 | 30.0 | 26.5 | 2731.4 | 8194.3 | 3 | 4,423 | 13,270 | 1 / 11 | |
| P1 | 10.0o | 10.0o | 20.02 | 20.0 | 16.16 | 20.33 | 25.42 | 26.5 | 0.7+0.38 | 2 / 11 | ||||||||
| P2 | 20.0o | 30.0o | 20.02 | 20.0 | 16.31 | 20.48 | 25.42 | 26.5 | 0.7+0.38 | 3 / 11 | ||||||||
| P3 | 20.0o | 50.0o | 20.23 | 20.2 | 16.60 | 20.77 | 25.42 | 26.5 | 0.7+0.38 | #2 | 20.0 | 26.5 | 2731.4 | 8677.2 | 4 | 3,830 | 15,319 | 4 / 11 |
| P4 | 16.0o | 66.0o | 20.56 | 20.6 | 16.90 | 21.07 | 25.42 | 26.5 | 0.7+0.38 | #3 | 16.0 | 26.5 | 2495.3 | 8194.3 | 6 | 3,149 | 18,892 | 5 / 11 |
| P5 | 24.0o | 90.0o | 21.31 | 21.1 | 17.42 | 21.59 | 25.42 | 26.5 | 0.7+0.38 | #4 | 64.0 | 26.5 | 2731.4 | 8840.6 | 18 | 4,666 | 83,996 | 6 / 11 |
| 40.0o | 130.0o | 21.97 | 22.0 | 18.25 | 22.42 | 25.42 | 26.5 | 0.7+0.38 | 8 / 11 | |||||||||
| P6 | 20.0o | 150.0o | 22.27 | 22.3 | 18.53 | 22.70 | 25.42 | 26.5 | 0.7+0.38 | #5 | 20.0 | 26.5 | 2731.4 | 8477.2 | 4 | 3,830 | 15,319 | 9 / 11 |
| P7 | 20.0o | 170.0o | 22.43 | 22.4 | 18.69 | 22.86 | 25.42 | 26.5 | 0.7+0.38 | #6 | 30.0 | 26.5 | 2731.4 | 8194.3 | 3 | 4,423 | 13,270 | 10 / 11 |
| P8 | 10.0o | 180.0o | 22.45 | 22.5 | 18.71 | 22.88 | 25.42 | 26.5 | 0.7+0.38 | 11 / 11 |
 S-Tank Engineering |
AAA Spherical Tank Calculation [1 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 0. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 1, Di = 15650 mm, CA = 3 mm, SG = 0.6215, Pg= 6.0 kg/cm²(=600 kPa), Pe= 1.01325 kg/cm²(=101.325 kPa), 수압테스트압력 GsetMAWP=808.3 kPa
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
4. Summary of Shell Thickness
Spherical tank, / External Pressure calc Result !! Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
4. Summary of Shell Thickness
| Segment | Each Angle | Angle α | 1.tdReq σeq | 2.tdReq ASME CODE | 3.ttReq MAWP Site | 4.ttReq MAP Shop | 5.teReq External Pressure | tUsed 결정 두께 | Forming Margin +0.7 mm | PNo | SEG. Angle | tUsed thick. | Width | Height | Qty | Unit WT | Net WT | |
| No. | deg. | deg. | mm | mm | mm | mm | mm | mm | mm | # | deg. | mm | mm | mm | SHT | kg/sht | kg | |
| 0 | 0o | 20.02 | 24.3 | 16.90 | 20.31 | 25.42 | 26.5 | 0.7+0.38 | #1 | 30.0 | 26.5 | 2731.4 | 8194.3 | 3 | 4,423 | 13,270 | 1 / 11 | |
| P1 | 10.0o | 10.0o | 20.02 | 24.3 | 16.92 | 20.34 | 25.42 | 26.5 | 0.7+0.38 | 2 / 11 | ||||||||
| P2 | 20.0o | 30.0o | 20.02 | 24.3 | 17.11 | 20.53 | 25.42 | 26.5 | 0.7+0.38 | 3 / 11 | ||||||||
| P3 | 20.0o | 50.0o | 20.23 | 24.6 | 17.47 | 20.88 | 25.42 | 26.5 | 0.7+0.38 | #2 | 20.0 | 26.5 | 2731.4 | 8677.2 | 4 | 3,830 | 15,319 | 4 / 11 |
| P4 | 16.0o | 66.0o | 20.56 | 25.0 | 17.85 | 21.26 | 25.42 | 26.5 | 0.7+0.38 | #3 | 16.0 | 26.5 | 2495.3 | 8194.3 | 6 | 3,149 | 18,892 | 5 / 11 |
| P5 | 24.0o | 90.0o | 21.32 | 25.6 | 18.50 | 21.91 | 25.42 | TD90USED | 0.7+0.16 | #4 | 64.0 | 27.5 | 2731.4 | 8840.6 | 18 | 4,843 | 87,165 | 6 / 11 |
| 40.0o | 130.0o | 21.97 | 26.7 | 19.54 | 22.95 | 25.42 | 27.5 | 0.7+0.07 | 8 / 11 | |||||||||
| P6 | 20.0o | 150.0o | 22.27 | 27.1 | 19.89 | 23.31 | 25.42 | 28.0 | 0.7+0.20 | #5 | 20.0 | 28.0 | 2731.4 | 8477.2 | 4 | 4,046 | 16,186 | 9 / 11 |
| P7 | 20.0o | 170.0o | 22.43 | 27.3 | 20.08 | 23.50 | 25.42 | 28.5 | 0.7+0.50 | #6 | 30.0 | 28.5 | 2731.4 | 8194.3 | 3 | 4,757 | 14,271 | 10 / 11 |
| P8 | 10.0o | 180.0o | 22.45 | 27.3 | 20.11 | 23.52 | 25.42 | 28.5 | 0.7+0.47 | 11 / 11 |
DivNo = 1, teReq = 25.42 mm; Pe :101.33 kPa ≤ Pa = 101.38 kPa = Factor_B / (Ro/tc)*1000 ; Factor_A=0.0625*tc/Rc = 0.0003570; Factor_B = 35.499 MPa
 S-Tank Engineering |
Spherical Tank Calculation [2 / ??? ] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : AAA3 | Rev. No. | [AAA4] | ||||||
1.1 At Design(Operating) Condition
D=15650 (cm), Sd=138 MPa, Pg=0.6 (MPa), HT_UPPCOL = 33700.0 (mm), deg_22 = 22.0 (deg), cos11 = 0.9816272 (rad)
Membrane Stres(By Roark Formula) Nθ=266.671 (N-mm), Nφ=31.757 (N-mm)
| No | Description | Symbol | Value | SI Unit | Value | Metric Unit | ||||
| 1 | Design Data : | |||||||||
| 2 | D = Tank In-Diameter | D = | 15650 | mm | 1565.0 | cm | ||||
| 3 | R = Inside Radius in Corroded Condition | R = | 7828 | mm | 782.8 | cm | ||||
| 4 | L = Design Liquid level | L = | 14080 | mm | 1408.0 | cm | ||||
| 5 | CA = Corrosion Allowance | CA = | 3.0 | mm | 0.3 | cm | ||||
| 6 | Wt = Total Weight at Operating Condition | Wt = | 13,279,549 | N | 1354137.2 | Kg | ||||
| 7 | S = Allowable Stress for the Design Condition SA516-70, Sd = 138MPa | S = | 138.0 | MPa | 1407.208 | Kg/cm² | ||||
| 8 | P = Design internal GAS Pressure | P = | 0.6 | MPa | 6.118 | Kg/cm² | ||||
| 9 | SG = Design Specific Gravity | SG = | 0.622 | 0.6215 | ||||||
| 10 | γ = Liquid Density | γ = | 6.094833E-6 | N/mm³ | 621.5 | Kg/m³ | ||||
| 11 | d = Outsdie diameter of Column | d = | 812.8 | mm | 81.28 | cm | ||||
| 12 | N = Number of Support Column | N = | 9.0 | columns | 9 | columns | ||||
| 13 | Δ = Angle of equator line to column top point | Δ = | 0.0 | degree | 0 | radians | ||||
| 14 | φ = Angle of upper column from top to base | φ = | 25.51015 | degree | 0.44524 | radians | ||||
| 15 | β = Angle of Liquid Level, β=Acos[(L+CA-R)/R] | β = | 36.96007 | degree | 0.64507 | radians | ||||
| 16 | C1 = cos(Δ + φ/2) / cos(11) | C1 = | 0.9935776 | 0.9935776 | ||||||
| 17 | C2 = Factor | C2 = | 1.0000000 | 1.0000000 | ||||||
| 18 | C3 = { sin(Δ+φ ) - sin(Δ) } / sin(22) | C3 = | 1.1496619 | 1.1496619 | ||||||
| 19 | C4 = sin(Δ+φ ) + sin(Δ) | C4 = | 0.4306709 | 0.4306709 | ||||||
| 20 | C5 = 22 / φ | C5 = | 0.8624020 | 0.8624020 | ||||||
| 21 | C6 = sin(Δ+φ) + sin(Δ) | C6 = | 0.4306709 | 0.4306709 | ||||||
| 22 | Calculation Result : | |||||||||
| 23 | PM = P×R/2 | PM = | 2348.4 | N-mm | 23.947 | Kg-cm | ||||
| 24 | Nθ = γR²/6 × [6×cosβ-6×cosθ-3×cosβ×cos²θ+4×cos³θ-cos³β)/(1-cos²θ)] | Nθ = | 266.671 | N-mm | 2.719 | Kg-cm | ||||
| 25 | Nφ = γR²/6 × [( cos³β - 3×cos²θ×cosβ + 2×cos³θ) / ( 1-cos²θ)] | Nφ = | 31.757 | N-mm | 0.324 | Kg-cm | ||||
| 26 | ΣNθ = Max. Latitude Membrane Force ΣNθ = Nθ + PM + VB - HB | ΣNθ = | 2761.52 | N/mm | 2815.967 | Kg/cm | ||||
| 27 | ΣNφ = Max. Meridional Membrane Force ΣNφ = Nφ + PM - IP | ΣNφ = | 2147.31 | N/mm | 2189.647 | Kg/cm | ||||
| 28 | Equator plate thk by Internal Pressure (by ASME Rules) | tASME = | 22.46 | mm | 2.246 | cm | ||||
| 29 | t(Point A) = Min. required thickness at point at A
| tReq = | 21.31 | mm | 2.131 | cm | ||||
| 30 | Effective equivalent stress(Von-Mises), σeq < S then OK
| σeq = | 123.257 | MPa | 1256.872 | Kg/cm² | ||||
| 31 | Calculation Result : | |||||||||
| 32 | Mo = Wt R cos(11) / N x { N / (2π)- 1 / (2 x Tan(π/N) ) } | Mo = | 665,041,909 | N-mm | 6781.54×103 | Kg-cm | ||||
| 33 | ΔMo = 3 Wt R / 4π × [ 0.2616 × ( 1+0.88196.4 × C5/N) / N + 0.02804 × ( 0.88196.4 × C5/N - 1 ) / C5 ] | ΔMo = | 240,795,336 | N-mm | 2455.429×103 | Kg-cm | ||||
| 34 | Mc = Wt R cos(11) / N x { 1 / 2 × sin(π/N)) - N / (2π) ) } | Mc = | 334,559,798 | N-mm | 3411.561×103 | Kg-cm | ||||
| 35 | ΔMc = 3 Wt R / 4π × [-0.5232 × ( 1+0.88196.4 × C5/N) / N + 0.02804 × ( 1 - 0.88196.4 × C5/N ) / C5 ] | ΔMc = | 112,331,238 | N-mm | 1145.46×103 | Kg-cm | ||||
| 36 | VB : Membrance Force resulting from longitudinal bending moment VB = Mvs / Za × t | VB = | 198.006 | N/mm | 201.91 | Kg/cm | ||||
| 37 | Mvs = Mo × C1 - ΔMo × C3 | Mvs = | 383,937,518 | N-mm | 3915.073×103 | Kg-cm | ||||
| 38 | Mvm = Mc × C1 - ΔMc × C3 | Mvm = | 203,268,176 | N-mm | 2072.759×103 | Kg-cm | ||||
| 39 | Za = IH / LA × t | Za = | 45,566,951 | mm³ | 45.567×103 | cm³ | ||||
| 40 | IH = R³ × [ VI x sin( φ/2)² + HI x cos(φ/2)² ] | IH = | 3,323,586,510 | mm³ | 3323.587×103 | cm³ | ||||
| 41 | VI = φ / 2 + ( sinφ/2 × cosφ/2 ) - [ 4 x sin(Δ/2)² / φ ] | VI = | 2.4129E-5 | 2.4129E-5 | ||||||
| 42 | HI = φ / 2 - ( sinφ/2 × cosφ/2 ) | HI = | 7.28256E-3 | 7.28256E-3 | ||||||
| 43 | LA = { R×sinφ/2×sinφ/2 } / ( φ/2 ) ) | LA = | 1714.056 | mm | 171.406 | cm | ||||
| 44 | HB : Membrance Force resulting from latitude bending moment HB = Mks / Zv | HB = | 51.558 | N/mm | 52.575 | Kg/cm | ||||
| 45 | Mks = Mo x ( 18 / 4π ) × ( d / R ) × C1 × C5 × C6 | Mks = | 36,500,735 | N-mm | 372.204×103 | Kg-cm | ||||
| 46 | Mkm = Mc x ( 18 / 4π ) × ( d / R ) × C1 × C5 × C6 | Mkm = | 18,362,269 | N-mm | 187.243×103 | Kg-cm | ||||
| 47 | Zv = IV / Max(KA, KB) | Zv = | 707,956 | mm³ | 7079.563 | cm² | ||||
| 48 | IV = R³ × [ VI × cos( φ/2)² + HI × sin( φ/2)² ] | IV = | 181,292,990 | mm³ | 181.293×103 | cm³ | ||||
| 49 | KA = R × [ 1 - cosφ/2 × sinφ/2 / (φ/2) ] | KA = | 256.079 | mm | 25.608 | cm | ||||
| 50 | KB = R × [ cosφ/2 × sinφ/2 / (φ/2) - cosφ ] | KB = | 507.08 | mm | 50.708 | cm | ||||
| 51 | IP : Membrance Force resulting from shear stress IP = 9×Wt / ( 2πN·R ) × C5 | IP = | 232.843 | N/mm | 237.434 | Kg/cm | ||||
| 52 | τxy : Shear Force, τxy = ( S' - P' ) / D' | τxy = | 160.674 | N/mm | 163.842 | Kg/cm | ||||
| 53 | S' = Wt/N×[ 1 - ( 18/(4π)·d/R·C5·{cos(Δ) + cos(φ)} ) ] | S' = | 1,115,447 | N | 113744.0 | Kg | ||||
| 54 | P' = d/R×Wt×[ 3/(4π)×{cos(Δ) - cos(Δ+φ) } ] | P' = | 32091.645 | N | 3272.4 | Kg | ||||
| 55 | D' = 2×R×[sin(Δ+φ) - sinΔ](용접접촉부 길이) | D' = | 6742.584 | mm | 674.258 | cm |
piDeg=[25.510146359306425] piRad=[0.4452360466355415] SPH_IHI_EQPL_SHEAR.jsp SPH_IHI_EQPL_SHEAR()
1.1 At Design(Operating) Condition Equator Plate(A Point at 90 deg) Stress :
D=15650 (cm), Sd=138 MPa, Pg=0.6 (MPa), HT_UPPCOL = 33700.0 (mm), deg_22 = 22.0 (deg), cos11 = 0.9816272 (rad)
| 각도 Data | 최대 변형에너지 Theory 이론에 의한 검증 by, Effective equivalent Stress(Von-Mises) | ASME DESIN RULE 에 의한 두께 와 최대변형에너지 Theory(Von-Mises Stress) 에 의한 두께 계산의 평가 | Nθ, Nφ 계산상수 Coeif. | ||||||||||||||||||||||||
| Segment Angle | Hmm | Hd Liquid Depth | Static Head Ps | Total Pressure Pt=Pg+Ps | PM = P*R/2 | Nθ | Nφ | VB | HB | IP | τxy | ΣNθ | ΣNφ | σeq | 평가 | Sd | A)Shear tReq | B)ASME tReq | C)tu= Max(A,B) | A - B 두께차이 | Design Margin (%) | Nθ coef. | Nφ coef. | Nθ coef. / 6 | Nφ coef. / 6 | ||
| No | deg. | mm | mm | MPa | MPa | N/mm | N/mm | N/mm | N/mm | MPa | < OK! | MPa | mm | mm | mm | mm | % | ||||||||||
| 0 | 15656.0 | 0 | 0 | 0.6 | 2348.4 | 2348.40 | 2348.40 | 130.47 | < OK | 138 | 20.02 | 20.02 | 21.0 | 5.46 | 0 | 0 | 0 | 0 | |||||||||
| P1 | 10 | 15537.1 | 0 | 0 | 0.6 | 2348.4 | 2348.40 | 2348.40 | 130.47 | < OK | 138 | 20.02 | 20.02 | 21.0 | 5.46 | 0 | 0 | 0 | 0 | ||||||||
| P2 | 30 | 14607.2 | 0 | 0 | 0.6 | 2348.4 | 2348.40 | 2348.40 | 130.47 | < OK | 138 | 20.02 | 20.02 | 21.0 | 5.46 | 0 | 0 | 0 | 0 | ||||||||
| P3 | 50 | 12859.7 | 1223.3 | 0.0075 | 0.6075 | 2348.4 | 52.96 | 5.40 | 2401.36 | 2353.80 | 132.11 | < OK | 138 | 20.23 | 20.24 | 21.0 | 0.01 | 4.27 | 0.851 | 0.087 | 0.142 | 0.014 | |||||
| P4 | 66 | 11011.9 | 3071.1 | 0.0187 | 0.6187 | 2348.4 | 128.01 | 18.51 | 2476.41 | 2366.91 | 131.00 | < OK | 138 | 20.56 | 20.56 | 21.5 | 5.07 | 2.057 | 0.297 | 0.343 | 0.05 | ||||||
| P5 | 90 | 7828.0 | 6255.0 | 0.0381 | 0.6381 | 2348.4 | 266.67 | 31.76 | 198.01 | 51.56 | 232.84 | 160.67 | 2761.52 | 2147.31 | 129.58 | < OK | 138 | 21.31 | 21.11 | 22.5 | -0.20 | 6.10 | 4.284 | 0.51 | 0.714 | 0.085 | Column Attached Equator Plate |
| 130 | 2796.3 | 11286.7 | 0.0688 | 0.6688 | 2348.4 | 233.48 | 305.02 | 2581.88 | 2653.42 | 130.92 | < OK | 138 | 21.97 | 21.98 | 23.0 | 0.01 | 5.13 | 3.751 | 4.9 | 0.625 | 0.817 | ||||||
| P6 | 150 | 1048.8 | 13034.2 | 0.0794 | 0.6794 | 2348.4 | 298.13 | 323.74 | 2646.53 | 2672.14 | 129.73 | < OK | 138 | 22.27 | 22.28 | 23.5 | 0.01 | 5.99 | 4.789 | 5.201 | 0.798 | 0.867 | |||||
| P7 | 170 | 118.9 | 13964.1 | 0.0851 | 0.6851 | 2348.4 | 331.69 | 334.54 | 2680.09 | 2682.94 | 130.81 | < OK | 138 | 22.43 | 22.44 | 23.5 | 0.01 | 5.21 | 5.329 | 5.374 | 0.888 | 0.896 | |||||
| P8 | 180 | 0 | 14083.0 | 0.0858 | 0.6858 | 2348.4 | 335.95 | 335.95 | 2684.35 | 2684.35 | 130.94 | < OK | 138 | 22.45 | 22.46 | 23.5 | 0.01 | 5.11 | 5.397 | 5.397 | 0.9 | 0.9 | |||||

 S-Tank Engineering |
Spherical Tank Calculation [2 / ??? ] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : AAA3 | Rev. No. | [AAA4] | ||||||
1.2 At Hydrostatic-Test Condition
D=15650 (cm), Syt=234 MPa, MAWP=0.78 (MPa), HT_UPPCOL = 33800.0 (mm), deg_22 = 22.0 (deg), cos11 = 0.9816272 (rad)
Membrane Stres(By Roark Formula) Nθ=500.389 (N-mm), Nφ=100.078 (N-mm)
| No | Description | Symbol | Value | SI Unit | Value | Metric Unit | ||||
| 1 | Design Data : | |||||||||
| 2 | D = Tank In-Diameter | D = | 15650 | mm | 1565.0 | cm | ||||
| 3 | R = Inside Radius in Corroded Condition | R = | 7825 | mm | 782.5 | cm | ||||
| 4 | L = Hydrostatic-test Water Level | L = | 15650 | mm | 1565.0 | cm | ||||
| 5 | CA = Corrosion Allowance | CA = | 0.0 | mm | 0 | cm | ||||
| 6 | Wt = Total Weight at Operating Condition | Wt = | 20,659,047 | N | 2106636.5 | Kg | ||||
| 7 | S = Allowable Stress for the Design Condition SA516-70, Sd = 234MPa | S = | 234.0 | MPa | 2386.136 | Kg/cm² | ||||
| 8 | P = Design internal GAS Pressure | P = | 0.6 | MPa | 6.118 | Kg/cm² | ||||
| 9 | SG = Design Specific Gravity | SG = | 1.0 | 1 | ||||||
| 10 | γ = Liquid Density | γ = | 9.80665E-6 | N/mm³ | 1000.0 | Kg/m³ | ||||
| 11 | d = Outsdie diameter of Column | d = | 812.8 | mm | 81.28 | cm | ||||
| 12 | N = Number of Support Column | N = | 9.0 | columns | 9 | columns | ||||
| 13 | Δ = Angle of equator line to column top point | Δ = | 0.0 | degree | 0 | radians | ||||
| 14 | φ = Angle of upper column from top to base | φ = | 25.5913 | degree | 0.44665 | radians | ||||
| 15 | β = Angle of Liquid Level, β=Acos[(L+CA-R)/R] | β = | 0.0 | degree | 0 | radians | ||||
| 16 | C1 = cos(Δ + φ/2) / cos(11) | C1 = | 0.9934181 | 0.9934181 | ||||||
| 17 | C2 = Factor | C2 = | 1.0000000 | 1.0000000 | ||||||
| 18 | C3 = { sin(Δ+φ ) - sin(Δ) } / sin(22) | C3 = | 1.1530734 | 1.1530734 | ||||||
| 19 | C4 = sin(Δ+φ ) + sin(Δ) | C4 = | 0.4319489 | 0.4319489 | ||||||
| 20 | C5 = 22 / φ | C5 = | 0.8596670 | 0.8596670 | ||||||
| 21 | C6 = sin(Δ+φ) + sin(Δ) | C6 = | 0.4319489 | 0.4319489 | ||||||
| 22 | Calculation Result : | |||||||||
| 23 | PM = P×R/2 | PM = | 2347.5 | N-mm | 23.938 | Kg-cm | ||||
| 24 | Nθ = γR²/6 × [6×cosβ-6×cosθ-3×cosβ×cos²θ+4×cos³θ-cos³β)/(1-cos²θ)] | Nθ = | 500.389 | N-mm | 5.103 | Kg-cm | ||||
| 25 | Nφ = γR²/6 × [( cos³β - 3×cos²θ×cosβ + 2×cos³θ) / ( 1-cos²θ)] | Nφ = | 100.078 | N-mm | 1.021 | Kg-cm | ||||
| 26 | ΣNθ = Max. Latitude Membrane Force ΣNθ = Nθ + PM + VB - HB | ΣNθ = | 3074.71 | N/mm | 3135.332 | Kg/cm | ||||
| 27 | ΣNφ = Max. Meridional Membrane Force ΣNφ = Nφ + PM - IP | ΣNφ = | 2086.35 | N/mm | 2127.485 | Kg/cm | ||||
| 28 | Equator plate thk by Internal Pressure (by ASME Rules) | tASME = | 12.6 | mm | 1.26 | cm | ||||
| 29 | t(Point A) = Min. required thickness at point at A
| tReq = | 11.76 | mm | 1.176 | cm | ||||
| 30 | Effective equivalent stress(Von-Mises), σeq < S then OK
| σeq = | 203.92 | MPa | 2079.405 | Kg/cm² | ||||
| 31 | Calculation Result : | |||||||||
| 32 | Mo = Wt R cos(11) / N x { N / (2π)- 1 / (2 x Tan(π/N) ) } | Mo = | 1,034,211,828 | N-mm | 10546.026×103 | Kg-cm | ||||
| 33 | ΔMo = 3 Wt R / 4π × [ 0.2616 × ( 1+0.88196.4 × C5/N) / N + 0.02804 × ( 0.88196.4 × C5/N - 1 ) / C5 ] | ΔMo = | 373,184,492 | N-mm | 3805.423×103 | Kg-cm | ||||
| 34 | Mc = Wt R cos(11) / N x { 1 / 2 × sin(π/N)) - N / (2π) ) } | Mc = | 520,276,536 | N-mm | 5305.344×103 | Kg-cm | ||||
| 35 | ΔMc = 3 Wt R / 4π × [-0.5232 × ( 1+0.88196.4 × C5/N) / N + 0.02804 × ( 1 - 0.88196.4 × C5/N ) / C5 ] | ΔMc = | 174,165,027 | N-mm | 1775.989×103 | Kg-cm | ||||
| 36 | VB : Membrance Force resulting from longitudinal bending moment VB = Mvs / Za × t | VB = | 306.306 | N/mm | 312.345 | Kg/cm | ||||
| 37 | Mvs = Mo × C1 - ΔMo × C3 | Mvs = | 597,095,603 | N-mm | 6088.681×103 | Kg-cm | ||||
| 38 | Mvm = Mc × C1 - ΔMc × C3 | Mvm = | 316,027,050 | N-mm | 3222.579×103 | Kg-cm | ||||
| 39 | Za = IH / LA × t | Za = | 32,164,142 | mm³ | 32.164×103 | cm³ | ||||
| 40 | IH = R³ × [ VI x sin( φ/2)² + HI x cos(φ/2)² ] | IH = | 3,350,271,797 | mm³ | 3350.272×103 | cm³ | ||||
| 41 | VI = φ / 2 + ( sinφ/2 × cosφ/2 ) - [ 4 x sin(Δ/2)² / φ ] | VI = | 2.4514E-5 | 2.4514E-5 | ||||||
| 42 | HI = φ / 2 - ( sinφ/2 × cosφ/2 ) | HI = | 7.351823E-3 | 7.351823E-3 | ||||||
| 43 | LA = { R×sinφ/2×sinφ/2 } / ( φ/2 ) ) | LA = | 1718.668 | mm | 171.867 | cm | ||||
| 44 | HB : Membrance Force resulting from latitude bending moment HB = Mks / Zv | HB = | 79.489 | N/mm | 81.056 | Kg/cm | ||||
| 45 | Mks = Mo x ( 18 / 4π ) × ( d / R ) × C1 × C5 × C6 | Mks = | 56,763,105 | N-mm | 578.823×103 | Kg-cm | ||||
| 46 | Mkm = Mc x ( 18 / 4π ) × ( d / R ) × C1 × C5 × C6 | Mkm = | 28,555,573 | N-mm | 291.186×103 | Kg-cm | ||||
| 47 | Zv = IV / Max(KA, KB) | Zv = | 714,103 | mm³ | 7141.03 | cm² | ||||
| 48 | IV = R³ × [ VI × cos( φ/2)² + HI × sin( φ/2)² ] | IV = | 183,950,286 | mm³ | 183.95×103 | cm³ | ||||
| 49 | KA = R × [ 1 - cosφ/2 × sinφ/2 / (φ/2) ] | KA = | 257.596 | mm | 25.76 | cm | ||||
| 50 | KB = R × [ cosφ/2 × sinφ/2 / (φ/2) - cosφ ] | KB = | 510.051 | mm | 51.005 | cm | ||||
| 51 | IP : Membrance Force resulting from shear stress IP = 9×Wt / ( 2πN·R ) × C5 | IP = | 361.224 | N/mm | 368.346 | Kg/cm | ||||
| 52 | τxy : Shear Force, τxy = ( S' - P' ) / D' | τxy = | 249.525 | N/mm | 254.445 | Kg/cm | ||||
| 53 | S' = Wt/N×[ 1 - ( 18/(4π)·d/R·C5·{cos(Δ) + cos(φ)} ) ] | S' = | 1,737,047 | N | 177129.5 | Kg | ||||
| 54 | P' = d/R×Wt×[ 3/(4π)×{cos(Δ) - cos(Δ+φ) } ] | P' = | 50257.224 | N | 5124.8 | Kg | ||||
| 55 | D' = 2×R×[sin(Δ+φ) - sinΔ](용접접촉부 길이) | D' = | 6760.0 | mm | 676.0 | cm |
piDeg=[25.59130479672834] piRad=[0.44665252858432775] SPH_IHI_EQPL_SHEAR.jsp SPH_IHI_EQPL_SHEAR()
1.2 At Hydrostatic-Test Condition Equator Plate(A Point at 90 deg) Stress :
D=15650 (cm), Syt=234 MPa, MAWP=0.78 (MPa), HT_UPPCOL = 33800.0 (mm), deg_22 = 22.0 (deg), cos11 = 0.9816272 (rad)
| 각도 Data | 최대 변형에너지 Theory 이론에 의한 검증 by, Effective equivalent Stress(Von-Mises) | ASME DESIN RULE 에 의한 두께 와 최대변형에너지 Theory(Von-Mises Stress) 에 의한 두께 계산의 평가 | Nθ, Nφ 계산상수 Coeif. | ||||||||||||||||||||||||
| Segment Angle | Hmm | Hd Liquid Depth | Static Head Ps | Total Pressure Pt=Pg+Ps | PM = P*R/2 | Nθ | Nφ | VB | HB | IP | τxy | ΣNθ | ΣNφ | σeq | 평가 | Sd | A)Shear tReq | B)ASME tReq | C)tu= Max(A,B) | A - B 두께차이 | Design Margin (%) | Nθ coef. | Nφ coef. | Nθ coef. / 6 | Nφ coef. / 6 | ||
| No | deg. | mm | mm | MPa | MPa | N/mm | N/mm | N/mm | N/mm | MPa | < OK! | MPa | mm | mm | mm | mm | % | ||||||||||
| 0 | 15650.0 | 0 | 0 | 0.6 | 2347.5 | 2347.50 | 2347.50 | 213.41 | < OK | 234 | 10.03 | 10.03 | 11.0 | 8.80 | 0 | 0 | 0 | 0 | |||||||||
| P1 | 10 | 15531.1 | 118.9 | 0.0012 | 0.6012 | 2347.5 | 6.85 | 2.27 | 2354.35 | 2349.77 | 213.82 | < OK | 234 | 10.05 | 10.05 | 11.0 | 8.62 | 0.068 | 0.023 | 0.011 | 0.004 | ||||||
| P2 | 30 | 14601.6 | 1048.4 | 0.0103 | 0.6103 | 2347.5 | 60.82 | 19.63 | 2408.32 | 2367.13 | 217.09 | < OK | 234 | 10.21 | 10.21 | 11.0 | 7.23 | 0.608 | 0.196 | 0.101 | 0.033 | ||||||
| P3 | 50 | 12854.8 | 2795.2 | 0.0274 | 0.6274 | 2347.5 | 164.76 | 49.74 | 2512.26 | 2397.24 | 213.63 | < OK | 234 | 10.50 | 10.49 | 11.5 | -0.01 | 8.70 | 1.646 | 0.497 | 0.274 | 0.083 | |||||
| P4 | 66 | 11007.7 | 4642.3 | 0.0455 | 0.6455 | 2347.5 | 279.70 | 76.54 | 2627.20 | 2424.04 | 210.98 | < OK | 234 | 10.82 | 10.80 | 12.0 | -0.02 | 9.84 | 2.795 | 0.765 | 0.466 | 0.127 | |||||
| P5 | 90 | 7825.0 | 7825.0 | 0.0767 | 0.6767 | 2347.5 | 500.39 | 100.08 | 306.31 | 79.49 | 361.22 | 249.52 | 3074.71 | 2086.35 | 211.76 | < OK | 234 | 11.76 | 11.32 | 13.0 | -0.44 | 9.50 | 5 | 1 | 0.833 | 0.167 | Column Attached Equator Plate |
| 130 | 2795.2 | 12854.8 | 0.1261 | 0.7261 | 2347.5 | 435.71 | 550.73 | 2783.21 | 2898.23 | 218.65 | < OK | 234 | 12.15 | 12.14 | 13.0 | -0.01 | 6.56 | 4.354 | 5.503 | 0.726 | 0.917 | ||||||
| P6 | 150 | 1048.4 | 14601.6 | 0.1432 | 0.7432 | 2347.5 | 539.65 | 580.84 | 2887.15 | 2928.34 | 215.40 | < OK | 234 | 12.43 | 12.43 | 13.5 | 7.95 | 5.392 | 5.804 | 0.899 | 0.967 | ||||||
| P7 | 170 | 118.9 | 15531.1 | 0.1523 | 0.7523 | 2347.5 | 593.62 | 598.19 | 2941.12 | 2945.69 | 218.03 | < OK | 234 | 12.58 | 12.58 | 13.5 | 6.82 | 5.932 | 5.977 | 0.989 | 0.996 | ||||||
| P8 | 180 | 0 | 15650.0 | 0.1535 | 0.7535 | 2347.5 | 600.47 | 600.47 | 2947.97 | 2947.97 | 218.37 | < OK | 234 | 12.60 | 12.60 | 13.5 | 6.68 | 6 | 6 | 1 | 1 | ||||||

], CalcRpt[i][2]=[SPH_IHI_SHEAR.jsp CALC_SPH_COL_BRA_ACCY_WEIGHT()
● WEIGHT SUMMARY SPH_IHI_SHEAR.jsp CALC_SPH_COL_BRA_ACCY_WEIGHT() BRACE AXIAL-FORCE DESIGN DATA
MRA(sWt[tid][20][1])= 0
MRA(sWt[tid][20][2])= 0
MRA(sWt[tid][20][3])= 38
MRA(sWt[tid][20][4])= 0
MRA(sWt[tid][20][5])= 160064.008
MRA(sWt[tid][20][6])= 0
MRA(sWt[tid][20][7])= 0
MRA(sWt[tid][20][8])= 0
MRA(sWt[tid][20][9])= 15650
MRA(sWt[tid][20][10])= 769.446
UPPER COLUMN : cbMatl[tid][0] = null
LOWER COLUMN : cbMatl[tid][1] = null
BRACE cbMatl[tid][2] = null
| 1. gCol[tid][1] = | Column Q'ty | Nc = | 9 | Columns |  |
| 2. gCol[tid][2] = | Column OD | OD = | 812.8 | mm | |
| 3. gCol[tid][3] = | Column thk | thk = | 8.74 | mm | |
| 4. gCol[tid][4] = | Tank Height | Htank = | 10825 | mm | |
| 5. gCol[tid][5] = | Upper Column Height | UCHT = | 3380 | mm | |
| 6. gCol[tid][6] = | Lower Column Height | LCHT = | 7445 | mm | |
| 7. gCol[tid][7] = | Column P.C.D | PCD = | 15260 | mm | |
| 8. gCol[tid][8] = | Brace Angle | BRang = | 35.0319 | deg. | |
| 9. gCol[tid][9] = | Brace Angle of Tank center to Brace Center | BRang_CTR = | 12.818 | deg | |
| 10. gCol[tid][10] = | Column CA | CA = | 0 | mm | |
| 11. gCol[tid][11] = | Brace OD | BR_OD = | 0 | mm | |
| 12. gCol[tid][12] = | Brace Thk | BR_Thk = | 0 | mm | |
| 13. gCol[tid][13] = | Brace CA | BR_CA = | 0 | mm |
A) TANK 제작비/자재비/도장비/외주비 부문
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 |
| No. | Description | Main Material | Thk. and Size | Unit | QTY | Net Wt kg | Gross Wt kg | 자재비 | 제작비 | No |
| 1 | SHELL PLATE | SA516-70 | t26.5 ~ 26.5 | SHT | 38 | 160.064 | 195.278 | 000,000 | 000,000 | 1 |
| 2 | UPPER COLUMN(PLATE) (재고확인) | null | t26.5, t11×2853×3380 | SHT | 9 | 8.555 | 9.411 | 000,000 | 000,000 | 2 |
| 3 | LOWER COLUMN (PIPE) | null | Ø812.8×8.74t × 7445L | PCS | 9 | 11.612 | 11.612 | 000,000 | 000,000 | 3 |
| 4 | BRACE ( PIPE, θ= 35.0319 deg.) | null | Ø0×0t × 9092L | PCS | 18 | 000,000 | 000,000 | 4 | ||
| 5 | COLUMN ACC'Y (PLATE) | A36 OR SS400 | - | LOT | 000,000 | 000,000 | 5 | |||
| 6 | BASE PLATE & ANCHOR BOLT (NO SITE PWHT = NO SLIDEING PLATE) | By SPEC. | SEE. Bellow TABLE 4) | LOT | 000,000 | 000,000 | 6 | |||
| 7 | NOZZLE & MANHOLE(DIP. PIPE) | Forging | Assumed Qty : 19 | 19 | 000,000 | 000,000 | 7 | |||
| 8 | ROOF PLATFORM & STRINGER | CLIP:SA516-70(OR CS) | PLATE & SHAPE | LOT | 000,000 | 000,000 | 8 | |||
| 9 | WATER SPRAY (Only Proposal) | By SPEC. | PIPE & ACC'Y | 15 | 000,000 | 000,000 | 9 | |||
| 10 | INTERNAL LADDER (Only Proposal) | SA516-70 | PLATE & SHAPE | LOT | 000,000 | 000,000 | 10 | |||
| 11 | INSULATION (Only Proposal) | By SPEC. | - | LOT | 000,000 | 000,000 | 11 | |||
| 12 | GRAND TOTAL | 74 | 180.231 | 216.301 | 000,000 | 000,000 | 12 |
 S-Tank Engineering |
AAA Spherical Tank Calculation [3 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 2. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 2, Di = 25200 mm, CA = 1.5 mm, SG = 0.59, Pg= 8.335653 kg/cm2(=833.565 kPa), Pe= 1.01325 kg/cm2(=101.325 kPa), 수압테스트압력 GsetMAWP=1549.4 kPa
Material : SA537-CL2, EXTERNAL CHART NO. [CS-4], DTEMP = 68 ℃, Sd = 230 MPa, St = 394.25 MPa, Samb = 230 MPa, LSR = Samb/Sd = 1.0, Ft = 550 MPa, Fy = 415 MPa
1. Design (Operating) Condition
Material : SA537-CL2, EXTERNAL CHART NO. [CS-4], DTEMP = 68 ℃, Sd = 230 MPa, St = 394.25 MPa, Samb = 230 MPa, LSR = Samb/Sd = 1.0, Ft = 550 MPa, Fy = 415 MPa
1. Design (Operating) Condition
| Segment | Each Angle | Angle α | H | Hs | Ps | Pg | P =Ps+Pg | tShear | tdReq | tUsed | Forming Margin 0.7+α | Pmax MAWP | Pmax MAP | Min.MAWP 찾기 | MinMAP 찾기 | LSR=Sa/S | ||
| No. | deg. | deg. | mm | mmH2O | kPa | kPa | kPa | mm | mm | mm | mm | MPa | MPa | MPa | MPa | LSR | ||
| 0 | 0o | 25203.0 | 0 | 0 | 833.6 | 833.6 | 24.34 | 24.36 | 35.5 | 0.7+0.44 | 1.2395 | 1.2942 | 1.0 | σeq = 218.846 | 1 / 13 | |||
| P1 | 6.4o | 6.4o | 25124.5 | 0 | 0 | 833.6 | 24.34 | 24.36 | 35.5 | 0.7+0.44 | 1.2395 | 1.2942 | 1.0 | σeq = 218.846 | 2 / 13 | |||
| P2 | 12.8o | 19.2o | 24502.1 | 0 | 0 | 833.6 | 24.34 | 24.36 | 35.5 | 0.7+0.44 | 1.2395 | 1.2942 | 1.0 | σeq = 218.846 | 3 / 13 | |||
| P3 | 12.8o | 32.0o | 23288.2 | 0 | 0 | 833.6 | 24.34 | 24.36 | 35.5 | 0.7+0.44 | 1.2395 | 1.2942 | 1.0 | σeq = 218.846 | 4 / 13 | |||
| P4 | 9.5o | 41.5o | 22039.5 | 0 | 0 | 833.6 | 24.34 | 24.36 | 35.5 | 0.7+0.44 | 1.2395 | 1.2942 | 1.0 | σeq = 218.846 | 5 / 13 | |||
| P5 | 45.5o | 87.0o | 13261.0 | 7006.5 | 40.5 | 874.1 | 25.50 | 25.47 | 35.5 | 0.7+0.44 | 1.1990 | 1.2942 | 1.0 | σeq = 220.843 | 6 / 13 | |||
| P6 | 3.0o | 90.0o | 12601.5 | 7666.0 | 44.4 | 878.0 | 25.54 | 25.58 | 35.5 | 0.7+0.44 | 1.1951 | 1.2942 | 1.0 | σeq = 221.2 | 7 / 13 | |||
| 48.5o | 138.5o | 3163.5 | 17104.0 | 99.0 | 932.6 | 27.05 | 27.07 | 35.5 | 0.7+0.44 | 1.1405 | 1.2942 | 1.0 | σeq = 221.765 | 9 / 13 | ||||
| P7 | 9.5o | 148.0o | 1914.8 | 18352.7 | 106.2 | 939.8 | 27.25 | 27.27 | 35.5 | 0.7+0.44 | 1.1333 | 1.2942 | 1.0 | σeq = 219.322 | 10 / 13 | |||
| P8 | 12.8o | 160.8o | 700.9 | 19566.6 | 113.2 | 946.8 | 27.44 | 27.46 | 35.5 | 0.7+0.44 | 1.1263 | 1.2942 | 1.0 | σeq = 220.95 | 11 / 13 | |||
| P9 | 12.8o | 173.6o | 78.5 | 20189.0 | 116.8 | 950.4 | 27.54 | 27.56 | 35.5 | 0.7+0.44 | 1.1227 | 1.2942 | 1.0 | σeq = 221.789 | 12 / 13 | |||
| P10 | 6.4o | 180.0o | 0 | 20267.5 | 117.3 | 950.9 | 27.55 | 27.58 | 35.5 | 0.7+0.44 | 1.1222 | 1.2942 | 1.1222 | 1.2942 | 1.0 | σeq = 221.895 | 13 / 13 |
| ||||
 |
| Test Case | escription | Formula | symbol | Min Value | Unit | Hydrostatic Test Condition | Selected |
| 1 | Max. Allowable Working Pressue | MAWP = (D.P) = Pg | MAWP = | 0.8336 | MPa | At Site (Hot & Corroded) | Selected |
| 2 | Max. Allowable Working Pressue | MAWP = CalcMAWP(Each Shell) | MAWP = | 1.1222 | MPa | At Site (Hot & Corroded) | N/A |
| 3 | Max. Allowable Pressue | MAP = CalcMAP(Each Shell) | MAP = | 1.2942 | MPa | At Shop ( New & Cold ) | N/A |
 S-Tank Engineering |
AAA Spherical Tank Calculation [3 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 2. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 2, Di = 25200 mm, CA = 1.5 mm, SG = 0.59, Pg= 8.335653 kg/cm2(=833.565 kPa), Pe= 1.01325 kg/cm2(=101.325 kPa), 수압테스트압력 GsetMAWP=1402.8 kPa
Material : SA537-CL2, EXTERNAL CHART NO. [CS-4], DTEMP = 68 ℃, Sd = 230 MPa, St = 394.25 MPa, Samb = 230 MPa, LSR = Samb/Sd = 1.0, Ft = 550 MPa, Fy = 415 MPa
2. Hydrostatic-Test Condition (at Site) MAWP : Hot-Corroded
Material : SA537-CL2, EXTERNAL CHART NO. [CS-4], DTEMP = 68 ℃, Sd = 230 MPa, St = 394.25 MPa, Samb = 230 MPa, LSR = Samb/Sd = 1.0, Ft = 550 MPa, Fy = 415 MPa
2. Hydrostatic-Test Condition (at Site) MAWP : Hot-Corroded
| Segment | Each Angle | Angle α | H | Hs | Ps | Pset (Test Gage Pressure) | P =Ps+Pset | 1)ttReq Pg (Basis) | 2)ttReq MAWP | 3)ttReq MAP 공장수압 시에만사용 | tUsed | Pmax MAWP | Pmax MAP | ||
| No. | deg. | deg. | mm | mmH2O | kPa | kPa | kPa | mm | mm | mm | mm | MPa | MPa | ||
| 0 | 0o | 25200.0 | 0 | 0 | 1402.8 | 1402.8 | 16.66 | 22.44 | 25.88 | 35.5 | 1.2395 | 1.2942 | σeq = 362.185 | 1 / 13 | |
| P1 | 6.4o | 6.4o | 25121.5 | 78.5 | 0.8 | 1403.6 | 16.67 | 22.45 | 25.89 | 35.5 | 1.2395 | 1.2942 | σeq = 362.519 | 2 / 13 | |
| P2 | 12.8o | 19.2o | 24499.1 | 700.9 | 6.9 | 1409.7 | 16.77 | 22.55 | 25.99 | 35.5 | 1.2395 | 1.2942 | σeq = 365.18 | 3 / 13 | |
| P3 | 12.8o | 32.0o | 23285.4 | 1914.6 | 18.8 | 1421.6 | 16.96 | 22.74 | 26.18 | 35.5 | 1.2395 | 1.2942 | σeq = 370.414 | 4 / 13 | |
| P4 | 9.5o | 41.5o | 22036.8 | 3163.2 | 31.0 | 1433.8 | 17.16 | 22.93 | 26.37 | 35.5 | 1.2395 | 1.2942 | σeq = 363.333 | 5 / 13 | |
| P5 | 45.5o | 87.0o | 13259.4 | 11940.6 | 117.1 | 1519.9 | 18.54 | 24.31 | 27.75 | 35.5 | 1.1990 | 1.2942 | σeq = 377.92 | 6 / 13 | |
| P6 | 3.0o | 90.0o | 12600.0 | 12600.0 | 123.6 | 1526.4 | 18.64 | 24.42 | 27.86 | 35.5 | 1.1951 | 1.2942 | σeq = 374.196 | 7 / 13 | |
| 48.5o | 138.5o | 3163.2 | 22036.8 | 216.1 | 1618.9 | 20.12 | 25.90 | 29.34 | 35.5 | 1.1405 | 1.2942 | σeq = 367.53 | 9 / 13 | ||
| P7 | 9.5o | 148.0o | 1914.6 | 23285.4 | 228.4 | 1631.2 | 20.32 | 26.09 | 29.54 | 35.5 | 1.1333 | 1.2942 | σeq = 371.729 | 10 / 13 | |
| P8 | 12.8o | 160.8o | 700.9 | 24499.1 | 240.3 | 1643.1 | 20.51 | 26.28 | 29.73 | 35.5 | 1.1263 | 1.2942 | σeq = 375.855 | 11 / 13 | |
| P9 | 12.8o | 173.6o | 78.5 | 25121.5 | 246.4 | 1649.2 | 20.61 | 26.38 | 29.82 | 35.5 | 1.1227 | 1.2942 | σeq = 367.769 | 12 / 13 | |
| P10 | 6.4o | 180.0o | 0 | 25200.0 | 247.1 | 1649.9 | 20.62 | 26.39 | 29.84 | 35.5 | 1.1222 | 1.2942 | σeq = 368.031 | 13 / 13 |
| No. | MAWP and Hydrostatic-test gauge setting pressure | symbol | Value (MPa) | Test Gage Pressure (kg/cm2) | Hydro. Test Location | ||||||||||
| CASE 1 | Design Internal Pressue (Pg = MAWP, BASIS) | MAWP = Pg = | 0.8336 | at Site | |||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.25×MWAP×LSR | Pset(MAWP) = | 1.0420 | 10.6250 | ||||||||||||
| CASE 2 | (Hot & Corroded) At Site : Max. Allowable Working Pressue | MAWP = | 1.1222 | at Site | |||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.25×MWAP×LSR | Pset(MAWP) = | 1.4028 | 14.3046 | ||||||||||||
| CASE 3 | ( New & Cold ) At Shop : Max. Allowable Pressue | MAP = | 1.2942 | at Shop | |||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.25×MAP×LSR | Pset(MAP) = | 1.6178 | 16.4970 | ||||||||||||
 S-Tank Engineering |
AAA Spherical Tank Calculation [3 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 2. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 2, Di = 25200 mm, CA = 1.5 mm, SG = 0.59, Pg= 8.335653 kg/cm2(=833.565 kPa), Pe= 1.01325 kg/cm2(=101.325 kPa), 수압테스트압력 GsetMAWP=1402.8 kPa
Material : SA537-CL2, EXTERNAL CHART NO. [CS-4], DTEMP = 68 ℃, Sd = 230 MPa, St = 394.25 MPa, Samb = 230 MPa, LSR = Samb/Sd = 1.0, Ft = 550 MPa, Fy = 415 MPa
3. MAWP/MAP Calculation
Material : SA537-CL2, EXTERNAL CHART NO. [CS-4], DTEMP = 68 ℃, Sd = 230 MPa, St = 394.25 MPa, Samb = 230 MPa, LSR = Samb/Sd = 1.0, Ft = 550 MPa, Fy = 415 MPa
3. MAWP/MAP Calculation
| Segment | Each Angle | Angle α | H Liquid Level | Hd | Ps | Ht Test Water Level | Ht | Pst | tc = tUsed - CA | tUsed | Pmax MAWP | Pmax MAP | MEP | |
| No. | deg. | deg. | mm | mmH2O | kPa | mm | H2O | kPa | mm | mm | MPa | MPa | kPa | |
| 0 | 0o | 25203.0 | 0 | 0 | 25200.0 | 0 | 0 | 34.00 | 35.5 | 1.2395 | 1.2942 | 108.4495 | 1 / 13 | |
| P1 | 6.4o | 6.4o | 25124.5 | 0 | 0 | 25121.5 | 78.5 | 0.8 | 34.00 | 35.5 | 1.2395 | 1.2942 | 108.4495 | 2 / 13 |
| P2 | 12.8o | 19.2o | 24502.1 | 0 | 0 | 24499.1 | 700.9 | 6.9 | 34.00 | 35.5 | 1.2395 | 1.2942 | 108.4495 | 3 / 13 |
| P3 | 12.8o | 32.0o | 23288.2 | 0 | 0 | 23285.4 | 1914.6 | 18.8 | 34.00 | 35.5 | 1.2395 | 1.2942 | 108.4495 | 4 / 13 |
| P4 | 9.5o | 41.5o | 22039.5 | 0 | 0 | 22036.8 | 3163.2 | 31.0 | 34.00 | 35.5 | 1.2395 | 1.2942 | 108.4495 | 5 / 13 |
| P5 | 45.5o | 87.0o | 13261.0 | 7006.5 | 40.5 | 13259.4 | 11940.6 | 117.1 | 34.00 | 35.5 | 1.1990 | 1.2942 | 108.4495 | 6 / 13 |
| P6 | 3.0o | 90.0o | 12601.5 | 7666.0 | 44.4 | 12600.0 | 12600.0 | 123.6 | 34.00 | 35.5 | 1.1951 | 1.2942 | 108.4495 | 7 / 13 |
| 48.5o | 138.5o | 3163.5 | 17104.0 | 99.0 | 3163.2 | 22036.8 | 216.1 | 34.00 | 35.5 | 1.1405 | 1.2942 | 108.4495 | 9 / 13 | |
| P7 | 9.5o | 148.0o | 1914.8 | 18352.7 | 106.2 | 1914.6 | 23285.4 | 228.4 | 34.00 | 35.5 | 1.1333 | 1.2942 | 108.4495 | 10 / 13 |
| P8 | 12.8o | 160.8o | 700.9 | 19566.6 | 113.2 | 700.9 | 24499.1 | 240.3 | 34.00 | 35.5 | 1.1263 | 1.2942 | 108.4495 | 11 / 13 |
| P9 | 12.8o | 173.6o | 78.5 | 20189.0 | 116.8 | 78.5 | 25121.5 | 246.4 | 34.00 | 35.5 | 1.1227 | 1.2942 | 108.4495 | 12 / 13 |
| P10 | 6.4o | 180.0o | 0 | 20267.5 | 117.3 | 0 | 25200.0 | 247.1 | 34.00 | 35.5 | 1.1222 | 1.2942 | 108.4495 | 13 / 13 |
| No. | MAWP and Hydrostatic-test gauge setting pressure | symbol | Value (MPa) | Test Gage Pressure (kg/cm2) | Hydro. Test Location | ||||||||||
| CASE 1 | Design Internal Pressue (Pg = MAWP, BASIS) | MAWP = Pg = | 0.8336 | at Site | |||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.25×MWAP×LSR | Pset(MAWP) = | 1.0420 | 10.6250 | ||||||||||||
| CASE 2 | (Hot & Corroded) At Site : Max. Allowable Working Pressue | MAWP = | 1.1222 | at Site | |||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.25×MWAP×LSR | Pset(MAWP) = | 1.4028 | 14.3046 | ||||||||||||
| CASE 3 | ( New & Cold ) At Shop : Max. Allowable Pressue | MAP = | 1.2942 | at Shop | |||||||||||
| Hydrostatic-Test Gauge Setting Pressure, Pset = 1.25×MAP×LSR | Pset(MAP) = | 1.6178 | 16.4970 | ||||||||||||
| No. | MAEP and performance in vacuum | symbol | Value kPa | Value kg/cm2 | Material Chart No. | ||||||||||
| 1 | Design External Pressure | Pe = | 101.3250 | SA537-CL2 | |||||||||||
| Maximum. Allowable External Pressure | MAEP = | 108.4495 | 1.1059 | CS-4 | |||||||||||
| Pe < MAEP, OK | Pe < MAEP | OK | |||||||||||||
| This tank is safe in full vacuum(1 atm = 101.325 kPa) condition. Full Vacuum(1 atm = 101.325 kPa) < MAEP(MinMAEP=108.4495 kPa) | |||||||||||||||
 S-Tank Engineering |
AAA Spherical Tank Calculation [3 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 2. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 2, Di = 25200 mm, CA = 1.5 mm, SG = 0.59, Pg= 8.335653 kg/cm2(=833.565 kPa), Pe= 1.01325 kg/cm2(=101.325 kPa), 수압테스트압력 GsetMAWP=1402.8 kPa
Material : SA537-CL2, EXTERNAL CHART NO. [CS-4], DTEMP = 68 ℃, Sd = 230 MPa, St = 394.25 MPa, Samb = 230 MPa, LSR = Samb/Sd = 1.0, Ft = 550 MPa, Fy = 415 MPa
4. Summary of Shell Thickness
], CalcRpt[i][1]=[Material : SA537-CL2, EXTERNAL CHART NO. [CS-4], DTEMP = 68 ℃, Sd = 230 MPa, St = 394.25 MPa, Samb = 230 MPa, LSR = Samb/Sd = 1.0, Ft = 550 MPa, Fy = 415 MPa
4. Summary of Shell Thickness
| Segment | Each Angle | Angle α | 1.tdReq σeq | 2.tdReq ASME CODE | 3.ttReq MAWP Site | 4.ttReq MAP Shop | 5.teReq External Pressure | tUsed 결정 두께 | Forming Margin +0.7 mm | PNo | SEG. Angle | tUsed thick. | Width | Height | Qty | Unit WT | Net WT | |
| No. | deg. | deg. | mm | mm | mm | mm | mm | mm | mm | # | deg. | mm | mm | mm | SHT | kg/sht | kg | |
| 0 | 0o | 24.34 | 24.4 | 22.44 | 25.88 | 34.36 | 35.5 | 0.7+0.44 | #1 | 19.2 | 35.5 | 2814.9 | 8444.6 | 3 | 6,293 | 18,879 | 1 / 13 | |
| P1 | 6.4o | 6.4o | 24.34 | 24.4 | 22.45 | 25.89 | 34.36 | 35.5 | 0.7+0.44 | 2 / 13 | ||||||||
| P2 | 12.8o | 19.2o | 24.34 | 24.4 | 22.55 | 25.99 | 34.36 | 35.5 | 0.7+0.44 | 3 / 13 | ||||||||
| P3 | 12.8o | 32.0o | 24.34 | 24.4 | 22.74 | 26.18 | 34.36 | 35.5 | 0.7+0.44 | #2 | 12.8 | 35.5 | 2814.9 | 9642.7 | 4 | 5,840 | 23,361 | 4 / 13 |
| P4 | 9.5o | 41.5o | 24.34 | 24.4 | 22.93 | 26.37 | 34.36 | 35.5 | 0.7+0.44 | #3 | 9.5 | 35.5 | 1873.5 | 8796.5 | 9 | 3,061 | 27,546 | 5 / 13 |
| P5 | 45.5o | 87.0o | 25.50 | 25.5 | 24.31 | 27.75 | 34.36 | 35.5 | 0.7+0.44 | #4 | 45.5 | 35.5 | 2823.6 | 10050.0 | 28 | 6,916 | 193,649 | 6 / 13 |
| P6 | 3.0o | 90.0o | 25.54 | 25.6 | 24.42 | 27.86 | 34.36 | 35.5 | 0.7+0.44 | #5 | 51.5 | 35.5 | 2827.4 | 11425.4 | 28 | 7,955 | 222,746 | 7 / 13 |
| 48.5o | 138.5o | 27.05 | 27.1 | 25.90 | 29.34 | 34.36 | 35.5 | 0.7+0.44 | 9 / 13 | |||||||||
| P7 | 9.5o | 148.0o | 27.25 | 27.3 | 26.09 | 29.54 | 34.36 | 35.5 | 0.7+0.44 | #6 | 9.5 | 35.5 | 1873.5 | 8796.5 | 9 | 3,061 | 27,546 | 10 / 13 |
| P8 | 12.8o | 160.8o | 27.44 | 27.5 | 26.28 | 29.73 | 34.36 | 35.5 | 0.7+0.44 | #7 | 12.8 | 35.5 | 2814.9 | 9442.7 | 4 | 5,840 | 23,361 | 11 / 13 |
| P9 | 12.8o | 173.6o | 27.54 | 27.6 | 26.38 | 29.82 | 34.36 | 35.5 | 0.7+0.44 | #8 | 19.2 | 35.5 | 2814.9 | 8444.6 | 3 | 6,293 | 18,879 | 12 / 13 |
| P10 | 6.4o | 180.0o | 27.55 | 27.6 | 26.39 | 29.84 | 34.36 | 35.5 | 0.7+0.44 | 13 / 13 |
 S-Tank Engineering |
AAA Spherical Tank Calculation [2 / 3] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : 1. V-1110A/B | Rev. No. | [AAA4] | ||||||
Design Code : Div. 1, Di = 15650 mm, CA = 3 mm, SG = 0.6215, Pg= 6.0 kg/cm²(=600 kPa), Pe= 1.01325 kg/cm²(=101.325 kPa), 수압테스트압력 GsetMAWP=965 kPa
Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
4. Summary of Shell Thickness
Spherical tank, / External Pressure calc Result !! Material : SA516-70, EXTERNAL CHART NO. [CS-2], DTEMP = 68 ℃, Sd = 138 MPa, St = 234 MPa, Samb = 138 MPa, LSR = Samb/Sd = 1.0, Ft = 485 MPa, Fy = 260 MPa
4. Summary of Shell Thickness
| Segment | Each Angle | Angle α | 1.tdReq σeq | 2.tdReq ASME CODE | 3.ttReq MAWP Site | 4.ttReq MAP Shop | 5.teReq External Pressure | tUsed 결정 두께 | Forming Margin +0.7 mm | PNo | SEG. Angle | tUsed thick. | Width | Height | Qty | Unit WT | Net WT | |
| No. | deg. | deg. | mm | mm | mm | mm | mm | mm | mm | # | deg. | mm | mm | mm | SHT | kg/sht | kg | |
| 0 | 0o | 20.02 | 20.0 | 16.14 | 20.31 | 25.42 | 26.5 | 0.7+0.38 | #1 | 30.0 | 26.5 | 2731.4 | 8194.3 | 3 | 4,423 | 13,270 | 1 / 11 | |
| P1 | 10.0o | 10.0o | 20.02 | 20.0 | 16.16 | 20.33 | 25.42 | 26.5 | 0.7+0.38 | 2 / 11 | ||||||||
| P2 | 20.0o | 30.0o | 20.02 | 20.0 | 16.31 | 20.48 | 25.42 | 26.5 | 0.7+0.38 | 3 / 11 | ||||||||
| P3 | 20.0o | 50.0o | 20.23 | 20.2 | 16.60 | 20.77 | 25.42 | 26.5 | 0.7+0.38 | #2 | 20.0 | 26.5 | 2731.4 | 8677.2 | 4 | 3,830 | 15,319 | 4 / 11 |
| P4 | 16.0o | 66.0o | 20.56 | 20.6 | 16.90 | 21.07 | 25.42 | 26.5 | 0.7+0.38 | #3 | 16.0 | 26.5 | 2495.3 | 8194.3 | 6 | 3,149 | 18,892 | 5 / 11 |
| P5 | 24.0o | 90.0o | 21.31 | 21.1 | 17.42 | 21.59 | 25.42 | TD90USED | 0.7+0.38 | #4 | 64.0 | 26.5 | 2731.4 | 8840.6 | 18 | 4,666 | 83,996 | 6 / 11 |
| 40.0o | 130.0o | 21.97 | 22.0 | 18.25 | 22.42 | 25.42 | 26.5 | 0.7+0.38 | 8 / 11 | |||||||||
| P6 | 20.0o | 150.0o | 22.27 | 22.3 | 18.53 | 22.70 | 25.42 | 26.5 | 0.7+0.38 | #5 | 20.0 | 26.5 | 2731.4 | 8477.2 | 4 | 3,830 | 15,319 | 9 / 11 |
| P7 | 20.0o | 170.0o | 22.43 | 22.4 | 18.69 | 22.86 | 25.42 | 26.5 | 0.7+0.38 | #6 | 30.0 | 26.5 | 2731.4 | 8194.3 | 3 | 4,423 | 13,270 | 10 / 11 |
| P8 | 10.0o | 180.0o | 22.45 | 22.5 | 18.71 | 22.88 | 25.42 | 26.5 | 0.7+0.38 | 11 / 11 |
DivNo = 2, teReq = 34.36 mm; Pe :101.33 kPa ≤ Pa = 101.32 kPa = 2*Fha*(tc/Ro)*1000; Fhe=38.956; Fic=38.956 MPa; Fha=19.478 MPa; FS=2
 S-Tank Engineering |
Spherical Tank Calculation [3 / ??? ] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : AAA3 | Rev. No. | [AAA4] | ||||||
1.1 At Design(Operating) Condition
D=25200 (cm), Sd=230 MPa, Pg=0.8336 (MPa), HT_UPPCOL = 47900.0 (mm), deg_22 = 22.0 (deg), cos11 = 0.9816272 (rad)
Membrane Stres(By Roark Formula) Nθ=524.463 (N-mm), Nφ=34.475 (N-mm)
| No | Description | Symbol | Value | SI Unit | Value | Metric Unit | ||||
| 1 | Design Data : | |||||||||
| 2 | D = Tank In-Diameter | D = | 25200 | mm | 2520.0 | cm | ||||
| 3 | R = Inside Radius in Corroded Condition | R = | 12601.5 | mm | 1260.15 | cm | ||||
| 4 | L = Design Liquid level | L = | 20266 | mm | 2026.6 | cm | ||||
| 5 | CA = Corrosion Allowance | CA = | 1.5 | mm | 0.15 | cm | ||||
| 6 | Wt = Total Weight at Operating Condition | Wt = | 48,010,433 | N | 4895701.7 | Kg | ||||
| 7 | S = Allowable Stress for the Design Condition SA537-CL2, Sd = 230MPa | S = | 230.0 | MPa | 2345.347 | Kg/cm² | ||||
| 8 | P = Design internal GAS Pressure | P = | 0.834 | MPa | 8.5 | Kg/cm² | ||||
| 9 | SG = Design Specific Gravity | SG = | 0.59 | 0.59 | ||||||
| 10 | γ = Liquid Density | γ = | 5.785924E-6 | N/mm³ | 590.0 | Kg/m³ | ||||
| 11 | d = Outsdie diameter of Column | d = | 1066.8 | mm | 106.68 | cm | ||||
| 12 | N = Number of Support Column | N = | 14.0 | columns | 14 | columns | ||||
| 13 | Δ = Angle of equator line to column top point | Δ = | 0.0 | degree | 0 | radians | ||||
| 14 | φ = Angle of upper column from top to base | φ = | 22.34352 | degree | 0.38997 | radians | ||||
| 15 | β = Angle of Liquid Level, β=Acos[(L+CA-R)/R] | β = | 52.53041 | degree | 0.91683 | radians | ||||
| 16 | C1 = cos(Δ + φ/2) / cos(11) | C1 = | 0.9994128 | 0.9994128 | ||||||
| 17 | C2 = Factor | C2 = | 1.0000000 | 1.0000000 | ||||||
| 18 | C3 = { sin(Δ+φ ) - sin(Δ) } / sin(22) | C3 = | 1.0148212 | 1.0148212 | ||||||
| 19 | C4 = sin(Δ+φ ) + sin(Δ) | C4 = | 0.3801587 | 0.3801587 | ||||||
| 20 | C5 = 22 / φ | C5 = | 0.9846257 | 0.9846257 | ||||||
| 21 | C6 = sin(Δ+φ) + sin(Δ) | C6 = | 0.3801587 | 0.3801587 | ||||||
| 22 | Calculation Result : | |||||||||
| 23 | PM = P×R/2 | PM = | 5252.305 | N-mm | 53.559 | Kg-cm | ||||
| 24 | Nθ = γR²/6 × [6×cosβ-6×cosθ-3×cosβ×cos²θ+4×cos³θ-cos³β)/(1-cos²θ)] | Nθ = | 524.463 | N-mm | 5.348 | Kg-cm | ||||
| 25 | Nφ = γR²/6 × [( cos³β - 3×cos²θ×cosβ + 2×cos³θ) / ( 1-cos²θ)] | Nφ = | 34.475 | N-mm | 0.352 | Kg-cm | ||||
| 26 | ΣNθ = Max. Latitude Membrane Force ΣNθ = Nθ + PM + VB - HB | ΣNθ = | 5963.75 | N/mm | 6081.333 | Kg/cm | ||||
| 27 | ΣNφ = Max. Meridional Membrane Force ΣNφ = Nφ + PM - IP | ΣNφ = | 4902.97 | N/mm | 4999.638 | Kg/cm | ||||
| 28 | Equator plate thk by Internal Pressure (by ASME Rules) | tASME = | 27.58 | mm | 2.758 | cm | ||||
| 29 | t(Point A) = Min. required thickness at point at A
| tReq = | 25.54 | mm | 2.554 | cm | ||||
| 30 | Effective equivalent stress(Von-Mises), σeq < S then OK
| σeq = | 204.815 | MPa | 2088.532 | Kg/cm² | ||||
| 31 | Calculation Result : | |||||||||
| 32 | Mo = Wt R cos(11) / N x { N / (2π)- 1 / (2 x Tan(π/N) ) } | Mo = | 1,591,876,926 | N-mm | 16232.627×103 | Kg-cm | ||||
| 33 | ΔMo = 3 Wt R / 4π × [ 0.2616 × ( 1+0.88196.4 × C5/N) / N + 0.02804 × ( 0.88196.4 × C5/N - 1 ) / C5 ] | ΔMo = | 626,437,627 | N-mm | 6387.886×103 | Kg-cm | ||||
| 34 | Mc = Wt R cos(11) / N x { 1 / 2 × sin(π/N)) - N / (2π) ) } | Mc = | 797,947,741 | N-mm | 8136.802×103 | Kg-cm | ||||
| 35 | ΔMc = 3 Wt R / 4π × [-0.5232 × ( 1+0.88196.4 × C5/N) / N + 0.02804 × ( 1 - 0.88196.4 × C5/N ) / C5 ] | ΔMc = | 301,626,804 | N-mm | 3075.737×103 | Kg-cm | ||||
| 36 | VB : Membrance Force resulting from longitudinal bending moment VB = Mvs / Za × t | VB = | 245.312 | N/mm | 250.149 | Kg/cm | ||||
| 37 | Mvs = Mo × C1 - ΔMo × C3 | Mvs = | 955,219,973 | N-mm | 9740.533×103 | Kg-cm | ||||
| 38 | Mvm = Mc × C1 - ΔMc × C3 | Mvm = | 491,381,902 | N-mm | 5010.701×103 | Kg-cm | ||||
| 39 | Za = IH / LA × t | Za = | 110,976,170 | mm³ | 110.976×103 | cm³ | ||||
| 40 | IH = R³ × [ VI x sin( φ/2)² + HI x cos(φ/2)² ] | IH = | 9,447,028,349 | mm³ | 9447.028×103 | cm³ | ||||
| 41 | VI = φ / 2 + ( sinφ/2 × cosφ/2 ) - [ 4 x sin(Δ/2)² / φ ] | VI = | 1.2458E-5 | 1.2458E-5 | ||||||
| 42 | HI = φ / 2 - ( sinφ/2 × cosφ/2 ) | HI = | 4.904588E-3 | 4.904588E-3 | ||||||
| 43 | LA = { R×sinφ/2×sinφ/2 } / ( φ/2 ) ) | LA = | 2426.109 | mm | 242.611 | cm | ||||
| 44 | HB : Membrance Force resulting from latitude bending moment HB = Mks / Zv | HB = | 58.329 | N/mm | 59.479 | Kg/cm | ||||
| 45 | Mks = Mo x ( 18 / 4π ) × ( d / R ) × C1 × C5 × C6 | Mks = | 72,212,762 | N-mm | 736.365×103 | Kg-cm | ||||
| 46 | Mkm = Mc x ( 18 / 4π ) × ( d / R ) × C1 × C5 × C6 | Mkm = | 36,197,528 | N-mm | 369.112×103 | Kg-cm | ||||
| 47 | Zv = IV / Max(KA, KB) | Zv = | 1,238,029 | mm³ | 12380.29 | cm² | ||||
| 48 | IV = R³ × [ VI × cos( φ/2)² + HI × sin( φ/2)² ] | IV = | 392,425,006 | mm³ | 392.425×103 | cm³ | ||||
| 49 | KA = R × [ 1 - cosφ/2 × sinφ/2 / (φ/2) ] | KA = | 316.976 | mm | 31.698 | cm | ||||
| 50 | KB = R × [ cosφ/2 × sinφ/2 / (φ/2) - cosφ ] | KB = | 629.129 | mm | 62.913 | cm | ||||
| 51 | IP : Membrance Force resulting from shear stress IP = 9×Wt / ( 2πN·R ) × C5 | IP = | 383.813 | N/mm | 391.38 | Kg/cm | ||||
| 52 | τxy : Shear Force, τxy = ( S' - P' ) / D' | τxy = | 268.058 | N/mm | 273.343 | Kg/cm | ||||
| 53 | S' = Wt/N×[ 1 - ( 18/(4π)·d/R·C5·{cos(Δ) + cos(φ)} ) ] | S' = | 2,641,155 | N | 269322.9 | Kg | ||||
| 54 | P' = d/R×Wt×[ 3/(4π)×{cos(Δ) - cos(Δ+φ) } ] | P' = | 72849.193 | N | 7428.6 | Kg | ||||
| 55 | D' = 2×R×[sin(Δ+φ) - sinΔ](용접접촉부 길이) | D' = | 9581.14 | mm | 958.114 | cm |
piDeg=[22.34351511368315] piRad=[0.3899679052028861] SPH_IHI_EQPL_SHEAR.jsp SPH_IHI_EQPL_SHEAR()
1.1 At Design(Operating) Condition Equator Plate(A Point at 90 deg) Stress :
D=25200 (cm), Sd=230 MPa, Pg=0.8336 (MPa), HT_UPPCOL = 47900.0 (mm), deg_22 = 22.0 (deg), cos11 = 0.9816272 (rad)
| 각도 Data | 최대 변형에너지 Theory 이론에 의한 검증 by, Effective equivalent Stress(Von-Mises) | ASME DESIN RULE 에 의한 두께 와 최대변형에너지 Theory(Von-Mises Stress) 에 의한 두께 계산의 평가 | Nθ, Nφ 계산상수 Coeif. | ||||||||||||||||||||||||
| Segment Angle | Hmm | Hd Liquid Depth | Static Head Ps | Total Pressure Pt=Pg+Ps | PM = P*R/2 | Nθ | Nφ | VB | HB | IP | τxy | ΣNθ | ΣNφ | σeq | 평가 | Sd | A)Shear tReq | B)ASME tReq | C)tu= Max(A,B) | A - B 두께차이 | Design Margin (%) | Nθ coef. | Nφ coef. | Nθ coef. / 6 | Nφ coef. / 6 | ||
| No | deg. | mm | mm | MPa | MPa | N/mm | N/mm | N/mm | N/mm | MPa | < OK! | MPa | mm | mm | mm | mm | % | ||||||||||
| 0 | 25203.0 | 0 | 0 | 0.8336 | 5252.31 | 5252.31 | 5252.31 | 218.85 | < OK | 230 | 24.34 | 24.36 | 25.5 | 0.02 | 4.85 | 0 | 0 | 0 | 0 | ||||||||
| P1 | 6.4 | 25124.5 | 0 | 0 | 0.8336 | 5252.31 | 5252.31 | 5252.31 | 218.85 | < OK | 230 | 24.34 | 24.36 | 25.5 | 0.02 | 4.85 | 0 | 0 | 0 | 0 | |||||||
| P2 | 19.2 | 24502.1 | 0 | 0 | 0.8336 | 5252.31 | 5252.31 | 5252.31 | 218.85 | < OK | 230 | 24.34 | 24.36 | 25.5 | 0.02 | 4.85 | 0 | 0 | 0 | 0 | |||||||
| P3 | 32 | 23288.2 | 0 | 0 | 0.8336 | 5252.31 | 5252.31 | 5252.31 | 218.85 | < OK | 230 | 24.34 | 24.36 | 25.5 | 0.02 | 4.85 | 0 | 0 | 0 | 0 | |||||||
| P4 | 41.5 | 22039.5 | 0 | 0 | 0.8336 | 5252.31 | 5252.31 | 5252.31 | 218.85 | < OK | 230 | 24.34 | 24.36 | 25.5 | 0.02 | 4.85 | 0 | 0 | 0 | 0 | |||||||
| P5 | 87 | 13261.0 | 7006.5 | 0.0405 | 0.8741 | 5252.31 | 477.01 | 33.85 | 5729.31 | 5286.15 | 220.84 | < OK | 230 | 25.50 | 25.47 | 26.5 | -0.03 | 3.98 | 3.115 | 0.221 | 0.519 | 0.037 | |||||
| P6 | 90 | 12601.5 | 7666.0 | 0.0444 | 0.878 | 5252.31 | 524.46 | 34.48 | 245.31 | 58.33 | 383.81 | 268.06 | 5963.75 | 4902.97 | 221.20 | < OK | 230 | 25.54 | 25.57 | 26.5 | 0.03 | 3.83 | 3.425 | 0.225 | 0.571 | 0.038 | Column Attached Equator Plate |
| 138.5 | 3163.5 | 17104.0 | 0.0990 | 0.9326 | 5252.31 | 563.11 | 683.96 | 5815.42 | 5936.26 | 221.76 | < OK | 230 | 27.05 | 27.07 | 28.0 | 0.02 | 3.58 | 3.677 | 4.466 | 0.613 | 0.744 | ||||||
| P7 | 148 | 1914.8 | 18352.7 | 0.1062 | 0.9398 | 5252.31 | 633.20 | 704.92 | 5885.50 | 5957.22 | 219.32 | < OK | 230 | 27.25 | 27.27 | 28.5 | 0.02 | 4.64 | 4.135 | 4.603 | 0.689 | 0.767 | |||||
| P8 | 160.8 | 700.9 | 19566.6 | 0.1132 | 0.9468 | 5252.31 | 700.41 | 726.21 | 5952.72 | 5978.52 | 220.95 | < OK | 230 | 27.44 | 27.46 | 28.5 | 0.02 | 3.93 | 4.574 | 4.742 | 0.762 | 0.79 | |||||
| P9 | 173.6 | 78.5 | 20189.0 | 0.1168 | 0.9504 | 5252.31 | 734.57 | 737.44 | 5986.87 | 5989.74 | 221.79 | < OK | 230 | 27.54 | 27.56 | 28.5 | 0.02 | 3.57 | 4.797 | 4.816 | 0.799 | 0.803 | |||||
| P10 | 180 | 0 | 20267.5 | 0.1173 | 0.9509 | 5252.31 | 738.87 | 738.87 | 5991.17 | 5991.17 | 221.90 | < OK | 230 | 27.55 | 27.58 | 28.5 | 0.03 | 3.52 | 4.825 | 4.825 | 0.804 | 0.804 | |||||

 S-Tank Engineering |
Spherical Tank Calculation [3 / ??? ] | Page | [$CP] / [$TP] | |||||
| [AAA1] | [AAA2] | |||||||
| Doc. No. : AAA3 | Rev. No. | [AAA4] | ||||||
1.2 At Hydrostatic-Test Condition
D=25200 (cm), Syt=394.25 MPa, MAWP=1.042 (MPa), HT_UPPCOL = 48000.0 (mm), deg_22 = 22.0 (deg), cos11 = 0.9816272 (rad)
Membrane Stres(By Roark Formula) Nθ=1297.42 (N-mm), Nφ=259.484 (N-mm)
| No | Description | Symbol | Value | SI Unit | Value | Metric Unit | ||||
| 1 | Design Data : | |||||||||
| 2 | D = Tank In-Diameter | D = | 25200 | mm | 2520.0 | cm | ||||
| 3 | R = Inside Radius in Corroded Condition | R = | 12600 | mm | 1260.0 | cm | ||||
| 4 | L = Hydrostatic-test Water Level | L = | 25200 | mm | 2520.0 | cm | ||||
| 5 | CA = Corrosion Allowance | CA = | 0.0 | mm | 0 | cm | ||||
| 6 | Wt = Total Weight at Operating Condition | Wt = | 85,473,461 | N | 8715867.4 | Kg | ||||
| 7 | S = Allowable Stress for the Design Condition SA537-CL2, Sd = 394.25MPa | S = | 394.25 | MPa | 4020.231 | Kg/cm² | ||||
| 8 | P = Design internal GAS Pressure | P = | 0.834 | MPa | 8.5 | Kg/cm² | ||||
| 9 | SG = Design Specific Gravity | SG = | 1.0 | 1 | ||||||
| 10 | γ = Liquid Density | γ = | 9.80665E-6 | N/mm³ | 1000.0 | Kg/m³ | ||||
| 11 | d = Outsdie diameter of Column | d = | 1066.8 | mm | 106.68 | cm | ||||
| 12 | N = Number of Support Column | N = | 14.0 | columns | 14 | columns | ||||
| 13 | Δ = Angle of equator line to column top point | Δ = | 0.0 | degree | 0 | radians | ||||
| 14 | φ = Angle of upper column from top to base | φ = | 22.39269 | degree | 0.39083 | radians | ||||
| 15 | β = Angle of Liquid Level, β=Acos[(L+CA-R)/R] | β = | 0.0 | degree | 0 | radians | ||||
| 16 | C1 = cos(Δ + φ/2) / cos(11) | C1 = | 0.9993280 | 0.9993280 | ||||||
| 17 | C2 = Factor | C2 = | 1.0000000 | 1.0000000 | ||||||
| 18 | C3 = { sin(Δ+φ ) - sin(Δ) } / sin(22) | C3 = | 1.0169399 | 1.0169399 | ||||||
| 19 | C4 = sin(Δ+φ ) + sin(Δ) | C4 = | 0.3809524 | 0.3809524 | ||||||
| 20 | C5 = 22 / φ | C5 = | 0.9824636 | 0.9824636 | ||||||
| 21 | C6 = sin(Δ+φ) + sin(Δ) | C6 = | 0.3809524 | 0.3809524 | ||||||
| 22 | Calculation Result : | |||||||||
| 23 | PM = P×R/2 | PM = | 5251.68 | N-mm | 53.552 | Kg-cm | ||||
| 24 | Nθ = γR²/6 × [6×cosβ-6×cosθ-3×cosβ×cos²θ+4×cos³θ-cos³β)/(1-cos²θ)] | Nθ = | 1297.42 | N-mm | 13.23 | Kg-cm | ||||
| 25 | Nφ = γR²/6 × [( cos³β - 3×cos²θ×cosβ + 2×cos³θ) / ( 1-cos²θ)] | Nφ = | 259.484 | N-mm | 2.646 | Kg-cm | ||||
| 26 | ΣNθ = Max. Latitude Membrane Force ΣNθ = Nθ + PM + VB - HB | ΣNθ = | 6881.0 | N/mm | 7016.667 | Kg/cm | ||||
| 27 | ΣNφ = Max. Meridional Membrane Force ΣNφ = Nφ + PM - IP | ΣNφ = | 4829.28 | N/mm | 4924.495 | Kg/cm | ||||
| 28 | Equator plate thk by Internal Pressure (by ASME Rules) | tASME = | 17.28 | mm | 1.728 | cm | ||||
| 29 | t(Point A) = Min. required thickness at point at A
| tReq = | 15.66 | mm | 1.566 | cm | ||||
| 30 | Effective equivalent stress(Von-Mises), σeq < S then OK
| σeq = | 333.742 | MPa | 3403.221 | Kg/cm² | ||||
| 31 | Calculation Result : | |||||||||
| 32 | Mo = Wt R cos(11) / N x { N / (2π)- 1 / (2 x Tan(π/N) ) } | Mo = | 2,833,697,279 | N-mm | 28895.671×103 | Kg-cm | ||||
| 33 | ΔMo = 3 Wt R / 4π × [ 0.2616 × ( 1+0.88196.4 × C5/N) / N + 0.02804 × ( 0.88196.4 × C5/N - 1 ) / C5 ] | ΔMo = | 1,112,010,119 | N-mm | 11339.347×103 | Kg-cm | ||||
| 34 | Mc = Wt R cos(11) / N x { 1 / 2 × sin(π/N)) - N / (2π) ) } | Mc = | 1,420,425,352 | N-mm | 14484.308×103 | Kg-cm | ||||
| 35 | ΔMc = 3 Wt R / 4π × [-0.5232 × ( 1+0.88196.4 × C5/N) / N + 0.02804 × ( 1 - 0.88196.4 × C5/N ) / C5 ] | ΔMc = | 535,516,480 | N-mm | 5460.748×103 | Kg-cm | ||||
| 36 | VB : Membrance Force resulting from longitudinal bending moment VB = Mvs / Za × t | VB = | 435.074 | N/mm | 443.652 | Kg/cm | ||||
| 37 | Mvs = Mo × C1 - ΔMo × C3 | Mvs = | 1,700,945,657 | N-mm | 17344.819×103 | Kg-cm | ||||
| 38 | Mvm = Mc × C1 - ΔMc × C3 | Mvm = | 874,882,792 | N-mm | 8921.322×103 | Kg-cm | ||||
| 39 | Za = IH / LA × t | Za = | 84,055,443 | mm³ | 84.055×103 | cm³ | ||||
| 40 | IH = R³ × [ VI x sin( φ/2)² + HI x cos(φ/2)² ] | IH = | 9,504,219,121 | mm³ | 9504.219×103 | cm³ | ||||
| 41 | VI = φ / 2 + ( sinφ/2 × cosφ/2 ) - [ 4 x sin(Δ/2)² / φ ] | VI = | 1.2596E-5 | 1.2596E-5 | ||||||
| 42 | HI = φ / 2 - ( sinφ/2 × cosφ/2 ) | HI = | 4.936875E-3 | 4.936875E-3 | ||||||
| 43 | LA = { R×sinφ/2×sinφ/2 } / ( φ/2 ) ) | LA = | 2431.023 | mm | 243.102 | cm | ||||
| 44 | HB : Membrance Force resulting from latitude bending moment HB = Mks / Zv | HB = | 103.171 | N/mm | 105.205 | Kg/cm | ||||
| 45 | Mks = Mo x ( 18 / 4π ) × ( d / R ) × C1 × C5 × C6 | Mks = | 128,535,700 | N-mm | 1310.699×103 | Kg-cm | ||||
| 46 | Mkm = Mc x ( 18 / 4π ) × ( d / R ) × C1 × C5 × C6 | Mkm = | 64,430,089 | N-mm | 657.004×103 | Kg-cm | ||||
| 47 | Zv = IV / Max(KA, KB) | Zv = | 1,245,846 | mm³ | 12458.464 | cm² | ||||
| 48 | IV = R³ × [ VI × cos( φ/2)² + HI × sin( φ/2)² ] | IV = | 396,582,530 | mm³ | 396.583×103 | cm³ | ||||
| 49 | KA = R × [ 1 - cosφ/2 × sinφ/2 / (φ/2) ] | KA = | 318.324 | mm | 31.832 | cm | ||||
| 50 | KB = R × [ cosφ/2 × sinφ/2 / (φ/2) - cosφ ] | KB = | 631.784 | mm | 63.178 | cm | ||||
| 51 | IP : Membrance Force resulting from shear stress IP = 9×Wt / ( 2πN·R ) × C5 | IP = | 681.886 | N/mm | 695.33 | Kg/cm | ||||
| 52 | τxy : Shear Force, τxy = ( S' - P' ) / D' | τxy = | 476.558 | N/mm | 485.954 | Kg/cm | ||||
| 53 | S' = Wt/N×[ 1 - ( 18/(4π)·d/R·C5·{cos(Δ) + cos(φ)} ) ] | S' = | 4,705,228 | N | 479799.7 | Kg | ||||
| 54 | P' = d/R×Wt×[ 3/(4π)×{cos(Δ) - cos(Δ+φ) } ] | P' = | 130,274 | N | 13284.2 | Kg | ||||
| 55 | D' = 2×R×[sin(Δ+φ) - sinΔ](용접접촉부 길이) | D' = | 9600.0 | mm | 960.0 | cm |
piDeg=[22.39268780540163] piRad=[0.39082613057544163] SPH_IHI_EQPL_SHEAR.jsp SPH_IHI_EQPL_SHEAR()
1.2 At Hydrostatic-Test Condition Equator Plate(A Point at 90 deg) Stress :
D=25200 (cm), Syt=394.25 MPa, MAWP=1.042 (MPa), HT_UPPCOL = 48000.0 (mm), deg_22 = 22.0 (deg), cos11 = 0.9816272 (rad)
| 각도 Data | 최대 변형에너지 Theory 이론에 의한 검증 by, Effective equivalent Stress(Von-Mises) | ASME DESIN RULE 에 의한 두께 와 최대변형에너지 Theory(Von-Mises Stress) 에 의한 두께 계산의 평가 | Nθ, Nφ 계산상수 Coeif. | ||||||||||||||||||||||||
| Segment Angle | Hmm | Hd Liquid Depth | Static Head Ps | Total Pressure Pt=Pg+Ps | PM = P*R/2 | Nθ | Nφ | VB | HB | IP | τxy | ΣNθ | ΣNφ | σeq | 평가 | Sd | A)Shear tReq | B)ASME tReq | C)tu= Max(A,B) | A - B 두께차이 | Design Margin (%) | Nθ coef. | Nφ coef. | Nθ coef. / 6 | Nφ coef. / 6 | ||
| No | deg. | mm | mm | MPa | MPa | N/mm | N/mm | N/mm | N/mm | MPa | < OK! | MPa | mm | mm | mm | mm | % | ||||||||||
| 0 | 25200.0 | 0 | 0 | 0.8336 | 5251.68 | 5251.68 | 5251.68 | 362.18 | < OK | 394.25 | 13.32 | 13.33 | 14.5 | 0.01 | 8.13 | 0 | 0 | 0 | 0 | ||||||||
| P1 | 6.4 | 25121.5 | 78.5 | 0.0008 | 0.8344 | 5251.68 | 7.28 | 2.42 | 5258.96 | 5254.10 | 362.52 | < OK | 394.25 | 13.33 | 13.34 | 14.5 | 0.01 | 8.05 | 0.028 | 0.009 | 0.005 | 0.002 | |||||
| P2 | 19.2 | 24499.1 | 700.9 | 0.0069 | 0.8405 | 5251.68 | 65.16 | 21.44 | 5316.84 | 5273.12 | 365.18 | < OK | 394.25 | 13.43 | 13.44 | 14.5 | 0.01 | 7.37 | 0.251 | 0.083 | 0.042 | 0.014 | |||||
| P3 | 32 | 23285.4 | 1914.6 | 0.0188 | 0.8524 | 5251.68 | 179.05 | 57.52 | 5430.73 | 5309.20 | 370.41 | < OK | 394.25 | 13.62 | 13.63 | 14.5 | 0.01 | 6.05 | 0.69 | 0.222 | 0.115 | 0.037 | |||||
| P4 | 41.5 | 22036.8 | 3163.2 | 0.0310 | 0.8646 | 5251.68 | 297.81 | 93.04 | 5549.49 | 5344.72 | 363.33 | < OK | 394.25 | 13.82 | 13.82 | 15.0 | 7.84 | 1.148 | 0.359 | 0.191 | 0.06 | ||||||
| P5 | 87 | 13259.4 | 11940.6 | 0.1171 | 0.9507 | 5251.68 | 1217.29 | 258.13 | 6468.97 | 5509.81 | 377.92 | < OK | 394.25 | 15.34 | 15.20 | 16.0 | -0.14 | 4.14 | 4.691 | 0.995 | 0.782 | 0.166 | |||||
| P6 | 90 | 12600.0 | 12600.0 | 0.1236 | 0.9572 | 5251.68 | 1297.42 | 259.48 | 435.07 | 103.17 | 681.89 | 476.56 | 6881.00 | 4829.28 | 374.20 | < OK | 394.25 | 15.66 | 15.30 | 16.5 | -0.36 | 5.09 | 5 | 1 | 0.833 | 0.167 | Column Attached Equator Plate |
| 138.5 | 3163.2 | 22036.8 | 0.2161 | 1.0497 | 5251.68 | 1259.09 | 1463.87 | 6510.77 | 6715.55 | 367.53 | < OK | 394.25 | 16.78 | 16.79 | 18.0 | 0.01 | 6.78 | 4.852 | 5.641 | 0.809 | 0.94 | ||||||
| P7 | 148 | 1914.6 | 23285.4 | 0.2284 | 1.062 | 5251.68 | 1377.85 | 1499.38 | 6629.53 | 6751.06 | 371.73 | < OK | 394.25 | 16.97 | 16.98 | 18.0 | 0.01 | 5.71 | 5.31 | 5.778 | 0.885 | 0.963 | |||||
| P8 | 160.8 | 700.9 | 24499.1 | 0.2403 | 1.0739 | 5251.68 | 1491.75 | 1535.46 | 6743.43 | 6787.14 | 375.86 | < OK | 394.25 | 17.16 | 17.17 | 18.0 | 0.01 | 4.67 | 5.749 | 5.917 | 0.958 | 0.986 | |||||
| P9 | 173.6 | 78.5 | 25121.5 | 0.2464 | 1.08 | 5251.68 | 1549.62 | 1554.48 | 6801.30 | 6806.16 | 367.77 | < OK | 394.25 | 17.26 | 17.27 | 18.5 | 0.01 | 6.72 | 5.972 | 5.991 | 0.995 | 0.998 | |||||
| P10 | 180 | 0 | 25200.0 | 0.2471 | 1.0807 | 5251.68 | 1556.90 | 1556.90 | 6808.58 | 6808.58 | 368.03 | < OK | 394.25 | 17.27 | 17.28 | 18.5 | 0.01 | 6.65 | 6 | 6 | 1 | 1 | |||||

], CalcRpt[i][2]=[SPH_IHI_SHEAR.jsp CALC_SPH_COL_BRA_ACCY_WEIGHT()
● WEIGHT SUMMARY SPH_IHI_SHEAR.jsp CALC_SPH_COL_BRA_ACCY_WEIGHT() BRACE AXIAL-FORCE DESIGN DATA
MRA(sWt[tid][20][1])= 0
MRA(sWt[tid][20][2])= 0
MRA(sWt[tid][20][3])= 88
MRA(sWt[tid][20][4])= 0
MRA(sWt[tid][20][5])= 555967.238
MRA(sWt[tid][20][6])= 0
MRA(sWt[tid][20][7])= 0
MRA(sWt[tid][20][8])= 0
MRA(sWt[tid][20][9])= 25200
MRA(sWt[tid][20][10])= 1995.038
UPPER COLUMN : cbMatl[tid][0] = null
LOWER COLUMN : cbMatl[tid][1] = null
BRACE cbMatl[tid][2] = null
| 1. gCol[tid][1] = | Column Q'ty | Nc = | 14 | Columns |  |
| 2. gCol[tid][2] = | Column OD | OD = | 1066.8 | mm | |
| 3. gCol[tid][3] = | Column thk | thk = | 15.09 | mm | |
| 4. gCol[tid][4] = | Tank Height | Htank = | 15600 | mm | |
| 5. gCol[tid][5] = | Upper Column Height | UCHT = | 4800 | mm | |
| 6. gCol[tid][6] = | Lower Column Height | LCHT = | 10800 | mm | |
| 7. gCol[tid][7] = | Column P.C.D | PCD = | 24690 | mm | |
| 8. gCol[tid][8] = | Brace Angle | BRang = | 26.9628 | deg. | |
| 9. gCol[tid][9] = | Brace Angle of Tank center to Brace Center | BRang_CTR = | 11.5467 | deg | |
| 10. gCol[tid][10] = | Column CA | CA = | 0 | mm | |
| 11. gCol[tid][11] = | Brace OD | BR_OD = | 0 | mm | |
| 12. gCol[tid][12] = | Brace Thk | BR_Thk = | 0 | mm | |
| 13. gCol[tid][13] = | Brace CA | BR_CA = | 0 | mm |
A) TANK 제작비/자재비/도장비/외주비 부문
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 |
| No. | Description | Main Material | Thk. and Size | Unit | QTY | Net Wt kg | Gross Wt kg | 자재비 | 제작비 | No |
| 1 | SHELL PLATE | SA537-CL2 | t35.5 ~ 35.5 | SHT | 88 | 555.967 | 678.280 | 000,000 | 000,000 | 1 |
| 2 | UPPER COLUMN(PLATE) (재고확인) | null | t35.5, t17×3651×4800 | SHT | 14 | 37.359 | 41.095 | 000,000 | 000,000 | 2 |
| 3 | LOWER COLUMN (PIPE) | null | Ø1066.8×15.09t × 10800L | PCS | 14 | 59.174 | 59.174 | 000,000 | 000,000 | 3 |
| 4 | BRACE ( PIPE, θ= 26.9628 deg.) | null | Ø0×0t × 12117L | PCS | 28 | 000,000 | 000,000 | 4 | ||
| 5 | COLUMN ACC'Y (PLATE) | A36 OR SS400 | - | LOT | 000,000 | 000,000 | 5 | |||
| 6 | BASE PLATE & ANCHOR BOLT (NO SITE PWHT = NO SLIDEING PLATE) | By SPEC. | SEE. Bellow TABLE 4) | LOT | 000,000 | 000,000 | 6 | |||
| 7 | NOZZLE & MANHOLE(DIP. PIPE) | Forging | Assumed Qty : 19 | 19 | 000,000 | 000,000 | 7 | |||
| 8 | ROOF PLATFORM & STRINGER | CLIP:SA537-CL2(OR CS) | PLATE & SHAPE | LOT | 000,000 | 000,000 | 8 | |||
| 9 | WATER SPRAY (Only Proposal) | By SPEC. | PIPE & ACC'Y | 15 | 000,000 | 000,000 | 9 | |||
| 10 | INTERNAL LADDER (Only Proposal) | SA537-CL2 | PLATE & SHAPE | LOT | 000,000 | 000,000 | 10 | |||
| 11 | INSULATION (Only Proposal) | By SPEC. | - | LOT | 000,000 | 000,000 | 11 | |||
| 12 | GRAND TOTAL | 144 | 652.500 | 778.549 | 000,000 | 000,000 | 12 |
CODE_CALC() 여기에 들어 왔는지 확인 필요 m = [2] j = [5] mySum = [90.0] tUsed = [27.5]mm
]
sph.uAry.length = [2] uAry[0].length = [5]
sph.bAry.length = [38] bAry[0].length = [15]
sph.cAry.length = [36] cAry[0].length = [12]
sph.dAry.length = [36] dAry[0].length = [12]
tReq=[
| tReq = |
| + CA |
| Div.1 tReq = |
| + CA |
| Div.1 tReq = |
| + CA |
| Div.1 tReq = |
| + CA |
| Div.2 tReq = R · [ EXP( |
| ) - 1 ] + CA |
시작시간 = [2025-11-21 21:49:03.0167]
종료시간 = [2025-11-21 21:49:03.0211]
HTML END!!!