Horizontal Vessel Saddle Calculation

Vessel Volume & Level Calculation

Design Data Input :

Description	Symbol	Value	Unit
D : Shell Inside Diameter	D =		mm
L : Length of vessel (Tangent Line to Tangent Line)	L =		mm
H : Depth of head	H =		mm
A : Distance from tangent line	A =		mm
CA : Corrosion Allowance (Shell / Head / Inner Saddle Ring Stiff.)	CA =		mm
ts : Thickness of shell plate	ts =		mm
th : Thickness of head plate	th =		mm
b : Width of saddle	b =		mm
tw : Thickness of wear plate	tw =		mm
th : Width of wear plate	bWear =		mm
E : Joint Efficiency ( girth seam )	E =
MATL : Shell & Head Plate Material	MATL =
Et : Elastic Modulus of Shell Plate	Et =		MPa
S : Allowable stress	S =		MPa
Sy : Yield strength	Sy =		MPa
θ : Contact angle Saddle bearing angle	θ =		degree
Wo : Weight of operating condition	Wo =		Ton
Wt : Weight of Hydrostatic-test condition	Wt =		Ton
Wc : Weight of Corroded condition	Wc =		Ton
We : Weight of Empty condition	We =		Ton
Pi : Design Internal Pressure	Pi =		MPa
Pe : Design External Pressure	Pe =		MPa
T-Ring : (Inner) Saddle Ring Size : (H1000x20+400x20)	T-RING =

[ LOAD CASE 1 ] Wo : Weight of Operating condition, Wo= 273 Ton
Saddle Strength Calculation Result :
(1) Saddle calculations are based on "Stresses in Large Cylindrical Pressure Vessels on Two Saddle Supports" by L.P. Zick.[PDF 다운로드]

Description	Symbol	Value	Unit
D : Shell Inside Diameter	D =	6000.0	mm
L : Length of vessel (Tangent Line to Tangent Line)	L =	14680.0	mm
R : Radius of shell	R =	3000.0	mm
H : Depth of head	H =	3000.0	mm
A : Distance from tangent line	A =	840.0	mm
P : Internal design pressure	P =	0.554251	MPa
Wo : Weight of Operating condition, Wo= 273 Ton	Wo=Qo =	2677215	N
Q : Load on one saddle	Q = Wo / 2	1338608	N
CA : Corrosion Allowance (Shell / Head / Inner Saddle Ring Stiff.)	CA =	0.0	mm
ts : Thickness of shell plate	ts =	13.0	mm
th : Thickness of head plate	th =	9.0	mm
b : Width of saddle	b =	1000.0	mm
tw : Thickness of wear plate	tw =	22.0	mm
th : Width of wear plate	bWear =	862.0	mm
θ : Contact angle Saddle bearing angle	θ =	180.0	degree
	θ =	3.14159	radian
Ratio of ts/R	ts/R =	0.0043
A(=840.0) < R/2(=1500), Ratio of A/R	A/R =	0.28
Shell and wear plate material	MATL =	SA516-70
Shell Weld Joint Efficiency ( Girth Seam )	E =	1.0
Allowable stress	S =	213.3	MPa
Yield strength	Sy =	450.0	MPa
T-Ring : (Inner) Saddle Ring Size	T-RING =	T1000x20+400x20

[Table 1] Value of Constant K
⋅K1 = 3.14 if the shell is stiffened by ring or head (A < R/2) (만일 SHELL 이 HEAD 또는 Stiffener Ring 으로 보강 되었다면 K1=3.14 임 )
θ : Contact angle Saddle bearing angle θ = 180.0 deg

Contact θ(deg.)	K1	K2	K3	K4	K5	K6 (A/R=0.28)	K7	K8	K9	K10	K11
180	0.718	0.577	0.318	0.26	0.216	0.018	0.624	1.183	0.25	0.017	0.318

Description	Symbol	Value	Unit	Description
Stress due to internal pressure, Sp = P⋅R / (2⋅ts)	Sp =	63.952	MPa	Sp = P⋅R / (2⋅ts)
Stress due to external pressure, Spe = Pe⋅R / (2⋅ts)	Spe =	5.1923	MPa	Spe = Pe⋅R / (2⋅ts)
M1 = Bending Moment at saddles 　 = 2.91340722E8 N-mm	M1 =	291	KN-m
M2 = Bending Moment at shell midspan 　 = 2.736292469E9 N-mm	M2 =	2736	KN-m
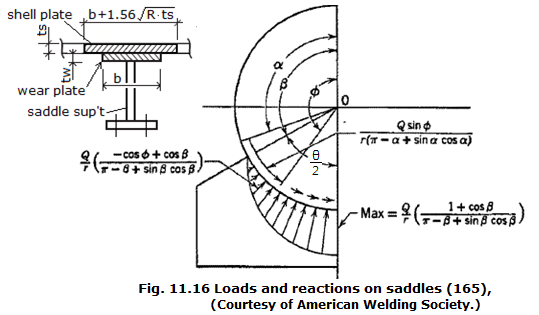
[ S1.a ] Longitudinal stress at saddle support - Without Stiffeners [내부 RING 보강 안됨]
Bending Moment of Saddle location	M1 =	291340722	N-mm	at saddle support
Coefficients K1	K1 =	0.718		A/R = 0.28 [TABLE 1]
Coefficients K8	K8 =	1.183		A/R = 0.28 [TABLE 1]
Longitudinal stress at Saddle(+ 인장), S1.a = (±)M1 / (K1 ⋅ R²⋅ t)	S1.a =	3.4681	MPa	S1.a = M1 / (K1 ⋅ R²⋅ t)
Longitudinal stress at Saddle(- 압축), S1.a = (-)M1 / (K8 ⋅ R²⋅ t)	S1.a =	-2.1049	MPa	S1.a = M1 / (K8 ⋅ R²⋅ t)
Maximum tensile stress, (+ 인장), S1t.a = S1.a + Sp	S1t.a =	67.4201	MPa	< St (213.3 MPa) OK
Maximum compressive stress (- 압축), S1c.a = -S1.a - Spe	S1c.a =	-3.0874	MPa	< Sc (59.47 MPa) OK
Tensile stress is acceptable ( S1t.a < St = 213.3 MPa )	St =	213.3	MPa	St = S ⋅ E
Compressive Stress is acceptable ( S1c.a < Sc = 59.47 MPa )	Sc =	59.47	MPa	Sc =Et/29 ⋅ (ts/R)⋅[2-(2/3)⋅100⋅(ts/R)]
[ S1.a ] Longitudinal stress at saddle support - With Stiffeners [내부 RING 보강 된 경우]
Bending Moment of Saddle location	M1 =	291340722	N-mm	at saddle support
M11 = 6⋅Q/12⋅[(8⋅A⋅H + 6⋅A² - 3⋅R² + 3⋅H²) / (3⋅L+4⋅H)]	M11 =	291340722	N-mm	at saddle support
Stress due to internal pressure, Sp = P⋅R / (2⋅ts)	Sp =	63.95	MPa	Sp = P⋅R / (2⋅ts)
Longitudinal stress at Saddle(+ 인장), S1t = (+)M1 / (π ⋅ R²⋅ t)	S1t =	(+) 0.7926	MPa	S1t = +M1 / (π ⋅ R²⋅ t)
Longitudinal stress at Saddle(- 압축), S1c = (-)M1 / (π ⋅ R²⋅ t)	S1c =	(-) 0.7926	MPa	S1c = -M1 / (π ⋅ R²⋅ t)
Maximum tensile stress, (+ 인장), S1t.a = S1t + Sp	S1t.a =	(+) 64.7447	MPa	< St (213.3 MPa) OK
Maximum compressive stress (- 압축), S1c.a = -S1c	S1c.a =	(-) 0.7926	MPa	< Sc (59.47 MPa) OK
[ S1.b ] Longitudinal stress at shell midspan
Bending Moment of Shell mid-point	M2 =	2736292469	N-mm	at shell center, Shell 중간지점
M22 = 3⋅Q/12⋅[(3⋅L²+6⋅R²-6⋅H²-12⋅A⋅L-16⋅A⋅H) / (3⋅L+4⋅H)]	M22 =	2736292469	N-mm	at shell center, Shell 중간지점
Longitudinal Stress at Shell Ceneter, S1.b = M2 / (π ⋅ R²⋅ t)	S1.b =	7.4443	MPa	S1.b = M2 / (π ⋅ R²⋅ t)
Maximum tensile stress, S1t.b = S1.b + Sp	S1t.b =	71.3964	MPa	< St (213.3 MPa) OK
Maximum compressive stress (shut down), S1c.b = -S1.b - Spe	S1c.b =	-12.6367	MPa	< Sc (59.47 MPa) OK
Tensile stress is acceptable ( S1t.b < St = 213.3 MPa )	St =	213.3	MPa	St = S ⋅ E
Compressive Stress is acceptable ( S1c.b < Sc = 59.47 MPa )	Sc =	59.4713	MPa	Sc =Et/29 ⋅ (ts/R)⋅[2-(2/3)⋅100⋅(ts/R)]
[ S2.a ] [접선 전단] Tangentinal shear stress on shell (S2) A = 840.0(mm) > R/2=1500.0 (mm)
Coefficients K2	K2 =	0.577		[TABLE 1]
at Shell [CASE a] A > R/2, S2a = K2⋅Q/R⋅ts ⋅ (L-2A/L+4/3H)	S2a =	14.5622	MPa	< 0.8·S (171 MPa) OK
at Shell [CASE b] A > R/2, S2b = K3⋅Q/R⋅ts ⋅ (L-2A/L+4/3H)	S2b =	8.0256	MPa	< 0.8·S (171 MPa) OK
[ S2.b ] [접선 전단] Tangentinal shear stress on shell (S2) A = 840.0(mm) ≤ R/2=1500.0 (mm)
Coefficients K4	K4 =	0.26		[TABLE 1]
Coefficients K5	K5 =	0.216		[TABLE 1]
at Shell [CASE d] A ≤ R/2, S2d = K4⋅Q / (R⋅ts)	S2d =	8.9241	MPa	< 0.8·S (171 MPa) OK
at Head [CASE e] A ≤ R/2, S2e = K4⋅Q / (R⋅th)	S2e =	12.8903	MPa	< 0.8·S (171 MPa) OK
at Addtional Stress at Head [CASE f] A ≤ R/2, S3 = K5⋅Q / (R⋅th)	S3 =	10.7089	MPa	< 1.25·S (267 MPa) OK
[ S4 ] Circumferential Bending Stress at the horn of saddle - shell not Stiffened [원주상 보강안됨, 원뿔부위] (S4)
Coefficients K2	K6 =	0.018		For Saddle contact angle θ=180.0 deg.[TABLE 1]
at Saddle Horn [CASE a] L ≥ 8R [보강안됨, 원뿔부위] S4a= -Q / [4⋅ts⋅( b+1.56⋅Sqrt(R⋅ts)] - [ 3⋅K6⋅Q / (2⋅ts²)]	S4a =	-233.54	MPa	< 1.5·S (320 MPa) OK
at Saddle Horn [CASE b] L < 8R [보강안됨, 원뿔부위] S4b= -Q / [4⋅ts⋅( b+1.56⋅Sqrt(R⋅ts)) - [ 12⋅K6⋅Q / (2⋅ts²)]	S4b =	-369.32	MPa	< 1.5·S (320 MPa) NG! 내부 RING 보강 필요
[ S5.a ] Circumferential compression Stress at bottom of Shell (S5.a : Wear Plate 가 없다고 가정하고 계산 한 것.)
Shell plate thickness	ts =	13	mm
Wear plate thickness	tw =	22	mm
Saddle Width	b =	1000	mm
Coefficients K7 =	K7 =	0.654
a) when, No Wear Plate S5 = Wear Plate 가 없다고 가정하고 계산 한 것. Note: ts = ts + tw only if wear plate is attached to shell and width of wear plate is a min. of b+1.56⋅Sqrt((R⋅ts)) Width of wear plate S5a = -K7 ⋅ Q / [ts ⋅ (b+1.56⋅Sqrt(R⋅ts))]	S5a =	-51.45	MPa	< 0.5Sy (225 MPa) OK
[ S5.b ] Stress at bottom of Shell, Wear plate-Ring compression in shell over saddle (S5.b : Wear Plate가 있을 경우)
Attached angle of wear plate	α =	95	degree
Combind Thickness of shell wear plate thickness	tw =	22	mm
Width of wear plate,	bWear =	862	mm
Effective Section Area Aeff = ts⋅ [b+1.56⋅Sqrt(R⋅ts)]+ tw⋅bWear	Aeff =	45556	mm²

Coefficients K7 =	K7 =	0.654
b) Stress at bottom of Shell, Wear plate-Ring compression, S5b = -K7⋅Q / Aeff	S5b =	-19.2	MPa	< 0.5Sy (225 MPa) OK
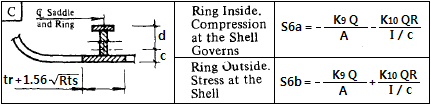
[ S6 ] Inner Ring Stiffener Stress at the saddle (S6), when Ring Stiffener Attached shell inside
Coefficients K9, K10 refer to P/V HANDBOOK page 95 Table.
Coefficients K9 when, θ = 160 degree.	K9 =	0.25
Coefficients K10 when, θ = 160 degree.	K10 =	0.017
	Acomb =	52927	mm²	Acomb= 318.0 cm2
	C =	509.5	mm	C1 = 56.32 mm, C2= 44.98 mm, b=32.31 mm
	R =	3000	mm
	Icomb =	8192000000	mm⁴	Ix= 448904.52 cm⁴
a) Ring Inside. Compression at the Shell Governs S6a = -(K9⋅Q / A) - [(K10⋅Q⋅R⋅C) / I]	S6a =	-10.57	MPa	< 1.0·S (213 MPa) OK
b) Ring Outside Stress at the Shell S6b = -(K9⋅Q / A) + [(K10⋅Q⋅R⋅C) / I]	S6b =	-2.08	MPa	< 0.5·S (225 MPa) OK

Stiffener Size : T1000x20+400x20　　　　Shell Section : t13 x 323 mm

No.	b	d	A=b⋅d	y	A⋅y	h = y-C1	Ah²	Ig=b⋅d³/12	SKETCH
No.	cm	cm	cm²	cm	cm³	(cm)	cm⁴	cm⁴
3	40.0	2.0	80.0	100.3	8024	43.98	154732.2	26.67
2	2.0	98.0	196.0	50.3	9858.8	-6.02	7105.48	156865.33
Shell	32.308	1.3	42.0	0.65	27.3	-55.67	130168.93	5.92
	SUM	∑ =	318		17910.1		292006.6	156897.92

C1	= ∑(AY) / ∑(A) (무게중심 위치)	C1 =	56.321	cm	무게중심에서 FLANGE 하단 까지 떨어진 거리
C2	= H - C1	C2 =	44.979	cm	무게중심에서 FLANGE 상단 까지 떨어진 거리
∑(A)	= Sum of Section Area (단면적)	∑(A)=	318.00	cm²	단면적 (빗금전체)
Ix	= ∑(Ah²) + ∑(Ig)	Ix =	448,905	cm⁴	X축 단면2차모멘트 (Moment of inertia)
Zx	= Ix / Max(C1, C2)	Zx =	7970.46	cm³	X축 단면계수 (Section Modulus)
Zmax	= Ix / Min(C1, C2)	Zmax =	9980.31	cm³	X축 (최대) 단면계수
Rx	= SQRT( Ix / A )	Rx =	37.57	cm	X축 회전반경
Ry	= SQRT( Iy / A )	Ry =	6.73	cm	Y축 회전반경
Section Area(Shell 포함)		Sarea =	318	cm²	Section Area(Shell 포함)
Ring 단면적 (Shell 제외)		ARing =	276	cm²	Ring 단면적 (Shell 제외)
Ring 원주길이		Leng =	6.11	m	Ring 길이(m) = 3.141592×(Di-C1)
Ring 단위중량 (kg/m),		WTm =	216.66	kg/m	단위중량(kg/m)
Ring Weight, Shell(1) 제외 중량		WT =	1323	kg	Ring 1 PCS 중량(kg)

0	M1 = Bending Moment at saddles 　 = 2.91340722E8 N-mm,	M1 =	2.91340722E8	N-mm, M1 = 291 KN-m
1	M2 = Bending Moment at shell midspan 　 = 2.736292469E9 N-mm,	M2 =	2.736292469E9	N-mm, M2 = 2736 KN-m
2	Sp = Stress due to internal pressure Sp = P⋅R / 2⋅ts	Sp =	63.95	MPa
3	S1 = Longitudinal bending at saddles - without stiffeners, tension (+인장) S1a = (＋) M1 / (K1 ⋅ R² ⋅ ts)	S1a =	(＋) 3.47	MPa
4	S2 = Longitudinal bending at saddles - without stiffeners, compression (-압축) S1b = (－) M1 / (K8 ⋅ R² ⋅ ts)	S1b =	(－) 2.1	MPa
5	S3 = Longitudinal bending at saddles - with stiffeners (+인장, -압축) S1c = (±) M1 / (π ⋅ R² ⋅ ts)	S1c =	( ± ) 0.79	MPa
6	S4 = Longitudinal bending at shell midspan, tension at bottom, compression at top (+인장, -압축) S1d = (±) M2 / (π ⋅ R² ⋅ ts)	S1d =	( ± ) 7.44	MPa
7	S5 = Tangential shear - shell stiffened in plane of saddle (내부 RING 에 의하여 보강됨) S5 = S2b = K3⋅Q/(π⋅R⋅ts) ⋅ [L-2A / L+4/3H]	S5=S2b=	8.03	MPa
8	S6 = Tangential shear - shell not stiffened, A > R/2 (보강안됨) S6 = S2a = K2⋅Q/(R⋅ts) ⋅ [L-2A / L+4/3H]	S6=S2a =	14.56	MPa
9	S7 = Tangential shear - shell not stiffened except by heads, A ≤ R/2 (보강안됨) S7 = S2d = K4⋅Q/(R⋅ts)	S7=S2d =	8.92	MPa
10	S8 = Tangential shear in head - shell not stiffened, A ≤ R/2 (보강안됨) S8 = S2e = K4⋅Q/(R⋅th)	S8=S2e =	12.89	MPa
11	S8a = Tangential shear in head , ( Addtional Stress ), A ≤ R/2 (보강안됨) S8a = S3 = K5⋅Q/(R⋅th)	S8a=S3 =	10.71	MPa
12	S8b = Tangential shear in head , 보강됨 OR A > R/2 = S8 = 0 MPa S8b = 0.0	S8b =	0.0	MPa
13	S9 = Circumferential bending at horn of saddle - shell not stiffened, L ≥ 8R S9=S4a= -Q / [4⋅ts⋅( b+1.56⋅Sqrt(R⋅ts)] - [ 3⋅K6⋅Q / (2⋅ts²)]	S9=S4a=	-233.54	MPa
14	S10 = Circumferential bending at horn of saddle - shell not stiffened, L < 8R S10=S4b= -Q / [4⋅ts⋅( b+1.56⋅Sqrt(R⋅ts)) - [ 12⋅K6⋅Q / (2⋅ts²)]	S10=S4b=	-369.32	MPa
15	S11 = Additional tension stress in head - shell not stiffened, A ≤ R/2 S11 = S3 = K5⋅Q/(R⋅th)	S11=S3 =	10.71	MPa
16	S12 = Circumferential compressive stress - stiffened or not stiffened, saddles attached or not) S12=S5a = -K7 ⋅ Q / (ts ⋅ [b+1.56⋅Sqrt(R⋅ts)]	S12=S5a =	-51.45	MPa
17	S13 = Circumferential stress in shell with stiffener in plane of saddle S13=S6a = -(K9⋅Q / Acomb) - [(K10⋅Q⋅R⋅c) / Icomb]	S13=S6a =	-10.57	MPa
18	S14 = Circumferential stress in ring stiffener S14=S6b = -(K9⋅Q / Acomb) + [(K10⋅Q⋅R⋅c) / Icomb]	S14=S6b =	-2.08	MPa

[Table 1] Value of Constant K [P/V handbook, Page No. 88]

Contact θ(deg.)	K1	K2	K3	K4	K5	K6 A=840.0 R=3000.0 A/R=0.28	K7	K8	K9	K10	K11
120	0.335	1.171	0.3183	0.88	0.401	0.018	0.76	0.603	0.34	0.053	0.204
122	0.345	1.139	0.3183	0.846	0.393	0.018	0.753	0.618	0.338	0.0514	0.2076
124	0.355	1.108	0.3183	0.813	0.385	0.018	0.746	0.634	0.336	0.0498	0.2112
126	0.366	1.078	0.3183	0.781	0.377	0.018	0.739	0.651	0.334	0.0482	0.2148
128	0.376	1.05	0.3183	0.751	0.369	0.018	0.732	0.669	0.332	0.0466	0.2184
130	0.387	1.022	0.3183	0.722	0.362	0.018	0.726	0.689	0.33	0.045	0.222
132	0.398	0.996	0.3183	0.694	0.355	0.018	0.72	0.705	0.328	0.0434	0.2258
134	0.409	0.971	0.3183	0.667	0.347	0.018	0.714	0.722	0.326	0.0418	0.2296
136	0.42	0.946	0.3183	0.641	0.34	0.018	0.708	0.74	0.324	0.0402	0.2334
138	0.432	0.923	0.3183	0.616	0.334	0.018	0.702	0.759	0.322	0.0386	0.2372
140	0.443	0.9	0.3183	0.592	0.327	0.018	0.697	0.78	0.32	0.037	0.241
142	0.455	0.879	0.3183	0.569	0.32	0.018	0.692	0.796	0.316	0.036	0.2446
144	0.467	0.858	0.3183	0.547	0.314	0.018	0.687	0.813	0.312	0.035	0.2482
146	0.48	0.837	0.3183	0.526	0.308	0.018	0.682	0.831	0.308	0.034	0.2518
148	0.492	0.818	0.3183	0.505	0.301	0.018	0.678	0.853	0.304	0.033	0.2554
150	0.505	0.799	0.3183	0.485	0.295	0.018	0.673	0.876	0.3	0.032	0.259
152	0.518	0.781	0.3183	0.466	0.289	0.018	0.669	0.894	0.298	0.0308	0.263
154	0.531	0.763	0.3183	0.448	0.283	0.018	0.665	0.913	0.296	0.0296	0.267
156	0.544	0.746	0.3183	0.43	0.278	0.018	0.661	0.933	0.294	0.0284	0.271
158	0.557	0.729	0.3183	0.413	0.272	0.018	0.657	0.954	0.292	0.0272	0.275
160	0.571	0.713	0.3183	0.396	0.266	0.018	0.654	0.976	0.29	0.026	0.279
162	0.585	0.698	0.3183	0.38	0.261	0.018	0.65	0.994	0.286	0.0252	0.2828
164	0.599	0.683	0.3183	0.365	0.256	0.018	0.647	1.013	0.282	0.0244	0.2866
166	0.613	0.668	0.3183	0.35	0.25	0.018	0.643	1.033	0.278	0.0236	0.2904
168	0.627	0.654	0.3183	0.336	0.245	0.018	0.64	1.054	0.274	0.0228	0.2942
170	0.642	0.64	0.3183	0.322	0.24	0.018	0.637	1.079	0.27	0.022	0.298
172	0.657	0.627	0.3183	0.309	0.235	0.018	0.635	1.097	0.266	0.021	0.302
174	0.672	0.614	0.3183	0.296	0.23	0.018	0.632	1.116	0.262	0.02	0.306
176	0.687	0.601	0.3183	0.283	0.225	0.018	0.629	1.137	0.258	0.019	0.31
178	0.702	0.589	0.3183	0.271	0.22	0.018	0.627	1.158	0.254	0.018	0.314
180	0.718	0.577	0.3183	0.26	0.216	0.018	0.624	1.183	0.25	0.017	0.318

매크로포함_SHI_SN2430_D12m_견적강도계산 (견적원가).xlsm - [PV4th SADDLES] Sheet 참고

Pressure Vessel Design Manulal (4th edition) / Table 4-27 Large diameter saddle supports

Vessel DIA.		BASE PLATE LENGTH	SADDLE HEIGHT	Bolt Hole Dia.	INNER RIB PITCH	BASE PLATE Width	BOLT PITCH	Saddle BTM Width	Saddle Top Width	Wear Plate Width	Rib Plate 두께	RIB 수량	BOLT 수량	Base Plate 두께	Gusset Plate 두께	Wear Plate 두께	Approx wt for 2 Saddles (kg)	Saddle RIB Height(Center)
DIA(ft)	DIA(mm)	A	B	D	E	F	G	GB=F-50.8	GT	H	J	N	n	tb	tg	tw	wt	h=B-D/2
14	4267	3937	2337	35	483	457	229	406	711	864	19	8	8	25	19	19	3175	203.2
15	4572	4343	2540	35	533	457	229	406	711	864	19	8	8	25	19	19	3629	254
16	4877	4648	2743	35	457	457	235	406	711	864	25	10	8	29	22	22	4536	304.8
17	5182	4902	2896	41	483	533	273	483	787	940	25	10	8	32	25	25	4990	304.8
18	5486	5258	3099	41	432	533	279	483	787	940	29	12	12	35	29	25	5443	355.6
20	6096	5258	3353	41	432	533	279	483	787	940	29	12	12	35	29	29	7031	304.8
22	6706	5563	3658	48	457	610	318	559	864	1016	32	12	12	38	32	32	8618	304.8
24	7315	6121	3962	48	432	610	318	559	864	1016	32	14	12	38	32	32	9979	304.8
26	7925	6477	4369	48	457	610	318	559	864	1016	35	14	12	41	32	32	11793	406.4
28	8534	6985	4674	54	432	686	356	635	940	1092	35	16	16	41	35	32	14061	406.4
30	9144	7823	4978	54	483	686	362	635	940	1092	38	16	16	44	38	35	16783	406.4
32	9754	8331	5283	54	457	686	362	635	940	1092	38	18	16	44	38	35	19958	406.4
34	10363	8788	5588	60	483	787	406	737	1041	1194	44	18	16	51	44	35	24494	406.4
36	10973	9246	5842	60	457	787	406	737	1041	1194	44	20	16	51	44	35	29937	355.6
38	11582	9754	6198	60	483	813	413	762	1067	1219	51	20	16	57	51	38	36287	406.4
40	12192	10262	6502	67	508	864	451	813	1118	1270	51	20	20	64	51	38	45359	406.4

Notes: [SADDLE STANDARD DWG(pdf)]
　1. All dimensions are in inches unless noted otherwise
　2. All saddles in this size range must be fully designed. The dimensions shown are a starting place or to be used for estimating only!
　3. Assume that anchor bolts diameter is d - 0.125, where d is the diameter of the hole. Assume that slots for sliding saddle are 6 d long.
　4. N = Number of ribs
　5. n = Number of anchor bolts

매크로포함_SHI_SN2430_D12m_견적강도계산 (견적원가).xlsm - [PV4th SADDLES] Sheet 참고

시작시간 = [2026-10-31 13:08:28.0119]
종료시간 = [2026-10-31 13:08:28.0124]

1출처 : Div2 SADDLE 계산서 [PDF COFFE] 2출처 : Div2 SADDLE 계산서 [PDF COFFE]
SADDLE 계산서 [PDFCOFFE] SITE
SADDLE 계산서 훌륭한 샘플 [DESIGN OF PRESSURE VESSEL SADDLE AND ZICK ANALYSIS]
SADDLE DESIGN UNDER OPERATING CONDITION_ASME Sec VIII Div 2 based on the Zick method.xlsx

Design Data Input :

Design Parameters	Symbol	Value	Unit
Design Temperature	T =	220	°C
Claculated Design Pressure	P =	1.471	MPa	15	kg/cm²g
Inside Shell Diameter	D =	4235	mm
Corosion Allowance	C =	3.2	mm
Corroded Inside Shell Diameter = (D + (2*C))	Dc =	4241.4	mm
Corroded Inside Shell Radius	R =	2120.7	mm
Corroded Shell thicknes	ts =	3.2	mm
Mean radius = (R + (ts/2)))	Rm =	2122.3	mm
Shell length (TL to TL)	L =	13253	mm
Head thickness	th =	28	mm
Thickness of wear plate	tr =	18	mm
Inside Depth of head in corroded condition	H =	1060.35	mm
Operating weight of the vessel	Wo =	2450377.8	N	249869	kg
Distance from Tangent line of vesel to Center of saddle	A =	800	mm
Distance from center line of vessel to bottom	B =	2200	mm
Number of saddle	n =	2	Nos.
Center of Saddle to saddel distance	Ls =	8953	mm
Length of base plate	E =	4370	mm
saddle width	b =	395	mm
Wear Plate width	b1 =	1200	mm
Joint Efficiency in shell	E =	0.85
Allowable stress value for shell material [As Per ASME Section - II, Part - D, Subpart 1, Table 1A]	S =	137.88	MPa		1406 kg/cm²
Allowable stress value for head material [As Per ASME Section - II, Part - D, Subpart 1, Table 1A]	S =	137.88	MPa		1406 kg/cm²
Sr Allowable stress value for R.F Pad (wear plate) Material [As Per ASME Section - II, Part - D, Subpart 1, Table 1A]	Sr =	137.88	MPa		1406 kg/cm²
Minimum Yield stress value for shell [As Per ASME Section - II, Part - D, Subpart 1, Table - Y1]	Sy =	260	MPa		2651.272 kg/cm²

Minimum Wear Plate Effective Width to be considered in analysis [b1']
b1' = min [b + 1.56 * Sqrt( Rm * ts ), 2a ]
b1' = min [ 395 + 1.56 * SQRT ( 2122.3 x 3.2 ) , 2 x 800 ] = 523.559 mm
Wear Pad Width 1200 mm is less than 1.56 * Sqrt(Rm*t) and less than 2a. The wear plate will be ignored.

AAA = [ASME SEC. VIII Div.2 Para. 4.15.3.2 Moment and Shear Force.
b1' = min[b + 1.56*sqrt( Rm*ts ), 2a ] = [523.60] mm
M₁ = [-6979614.46] N-mm
M₂ = [2913488877.01] N-mm
M_β = K7 * Q * Rm = [25805831.89] N-mm
M_β = K10 * Q * Rm = [-319016416.95] N-mm
Load, Q = [121529.00] N One Saddle 반력, maximum value of the reaction at the saddle support from weight and other loads as applicable.
Load, T = [1002477.81] N One Saddle 전단력, maximum shear force at the saddle
R = [2120.70] mm, Rm = [1807.50] mm,
ASME SEC. VIII Div.2 Para. 4.15.3.3 Longitudinal Stress.
σ₁ = [423.45] MPa < S*E = [117.20] MPa OK
σ₂ = [552.14] MPa < S*E = [117.20] MPa OK
σ₃ = [487.95] MPa < S*E = [117.20] MPa OK
σ₄ = [487.64] MPa < S*E = [117.20] MPa OK
σ₃* = [488.90] MPa < S*E = [117.20] MPa OK , K1 = [0.1393]
σ₄* = [487.17] MPa < S*E = [117.20] MPa OK , K1* = [0.2456]

ASME SEC. VIII Div.2 Para. 4.15.3.4 Shear Stresses.
τ₁ = [46.99] MPa < Min(0.8*S, 0.533*Sy) = [110.30] MPa OK , (a) The shear stress in the cylindrical shell with a stiffening ring
τ₂ = [134.55] MPa < Min(0.8*S, 0.533*Sy) = [110.30] MPa OK , (b) The shear stress in the cylindrical shell with stiffening rings on both sides of the saddle support
τ₃ = [112.22] MPa < Min(0.8*S, 0.533*Sy) = [110.30] MPa OK , (d)-(Eq. 4.15.13) The shear stress in the cylindrical shell without stiffening ring(s and For Spherical head (Formed Head )
τ₃* = [12.83] MPa < Min(0.8*S, 0.533*Sy) = [110.30] MPa OK , (d)-(Eq. 4.15.14) For 2:1 Ellipse head OR 10% Dish Head
ASME SEC. VIII Div.2 Para. 4.15.3.4 Shear Stresses.
σ₅ = [118.51] MPa < 1.25*S = [172.35] MPa OK (d)-(2) Eq. 4.15.16 Membrane stress in a torispherical or elliptical head acting as a stiffener, the coefficient K4 is given in

ASME SEC. VIII Div.2 Para. 4.15.3.5 Circumferential Stress.
(c) Circumferential stresses in the cylindrical shell without stiffening ring(s) = (CIRCUMFRENCIAL STRESSES WITHOUT WEAR PLATE)
(1) The maximum compressive circumferential membrane stress in the cylindrical shell at the base of the saddle support
σ₆ = [-52.7] MPa < S = [137.88] MPa OK
σ₇ = [0] MPa < S = [137.88] MPa OK
σ₇* = [-2470.12] MPa < S = [137.88] MPa OK
σ₆,r = [-3.47] MPa < S = [137.88] MPa OK
σ₇,r = [0] MPa < S = [137.88] MPa OK
σ₇,r* = [-64.39] MPa < S = [137.88] MPa OK
ASME SEC. VIII Div.2 Para. 4.15.3.5 Circumferential Stress. 내부 보강링이 있을 경우 샘플 : Saddle_Analysis ( ASME Div2 Examples ).pdf)
(d) Circumferential stresses in the cylindrical shell with a stiffening ring along the plane of the saddle support.
(1) The maximum compressive circumferential membrane stress in the cylindrical shell shall be computed using eq. (4.15.32). The coefficient K5 is given in Table 4.15.1.
σ₆* = [-85.27] MPa < S = [137.88] MPa OK
σ₈* = [0.00] MPa < S = [137.88] MPa OK
σ₉* = [0.00] MPa < S = [137.88] MPa OK

[Table 1] Value of Constant K [ASME Section VII, Div. 2, Fig 4.15.5, and Table 4.15.1]

Contact Angle (θ, deg)	K1	K1^*	K2	K3	K4	K5	K6	K7	K8	K9	K10
139	0.1393	0.2456	0.9115	0.604	0.3302	0.673	0.0317	0.0096	0.3021	-0.0722	-0.1191

ASME SEC. VIII Div.2 Para. 4.15.3 SADDLE SUPPORTS FOR HORIZONTAL VESSELS

0	Q =	121529	N	Eqn. 4.15.0
1	M₁ =	-6979614	N-mm	Eqn. 4.15.1
2	M₂ =	2913488877	N-mm	Eqn. 4.15.2
3	T =	1002478	N	Eqn. 4.15.3
4	σ₁ =	423.45	MPa	Eqn. 4.15.4
5	σ₂ =	552.14	MPa	Eqn. 4.15.5
6	σ₃ =	487.95	MPa	Eqn. 4.15.6
7	σ₄ =	487.64	MPa	Eqn. 4.15.7
8	σ₃* =	488.90	MPa	Eqn. 4.15.8
9	σ₄* =	487.17	MPa	Eqn. 4.15.9
10	Sc =	18.75	MPa	Eqn. 4.15.10
11	τ₁ =	46.99	MPa	Eqn. 4.15.11
12	τ₂ =	134.55	MPa	Eqn. 4.15.12
13	τ₃ =	112.22	MPa	Eqn. 4.15.13
14	τ₃* =	12.83	MPa	Eqn. 4.15.14
15	When, Torispherical Head, σ₅ =	62.76	MPa	Eqn. 4.15.15
16	When, 2:1 Ellipsoidal head, σ₅ =	118.51	MPa	Eqn. 4.15.16
17	Flat Colver, σ₅ =	0.00	MPa	Eqn. 4.15.17
18	Mβ =	25805832	N-mm	Eqn. 4.15.18
19	Mβ =	-319016417	N-mm	Eqn. 4.15.19
20	x1=x2 =	64.28	mm	Eqn. 4.15.20
21	σ₆ =	-52.70	MPa	Eqn. 4.15.21
22	If L ≥ 8*Rm, then σ₇ =	0.00	MPa	Eqn. 4.15.22
23	If L < 8Rm, then σ₇* =	-2470.12	MPa	Eqn. 4.15.23
24	b1 =	1200.00	mm	Eqn. 4.15.24
25	σ₆r =	-3.47	MPa	Eqn. 4.15.25
26	η =	1.00		Eqn. 4.15.26
27	θ1 = θ + θ / 12 =	150.58	deg.	Eqn. 4.15.27
28	σ₇,r =	0.00	MPa	Eqn. 4.15.28
29	σ₇*,r =	-64.39	MPa	Eqn. 4.15.29
30	If L ≥ 8*Rm, then σ₇,1 =	0.00	MPa	Eqn. 4.15.30
31	If L < 8Rm, then σ₇*,1 =	0.00	MPa	Eqn. 4.15.31
32	σ₆* =	-85.27	MPa	Eqn. 4.15.32
33	σ₈ =	1246.22	MPa	Eqn. 4.15.33
34	σ₉ =	-1625.57	MPa	Eqn. 4.15.34

]
ADDITIONAL LONGITUDINAL FORCES :- [As Per Dennis Moss, Page No. 256]
　　CASE A ) Pier Deflection, FL1 :

　　　　FL1 = Ks Y / n , Ks : N.R , Pier Spring Rate

　　　　This is not a case of Pier Deflection.

　　CASE B ) Expansion / Contraction due to Friction Load, FL2 :

　　　　μ = 0.06 friction coefficient of sliding Material [As Per Dennis Moss, Page No. 267]

　　　　FL2 = μ * Wo = 0.06 x 2451214.89 = 147072.89 N

　　　　[Teflon to Teflon friction]

　　CASE C ) Bundle Pulling Force (Load applies to fixed saddle) , Fp :
　　　　Fp = N.R , No additional Pulling force is applied

CALCULATION OF SADDLE REACTION FORCES, Q
　　FL = Wind Force towards longiudinal direction 4710 N
　　　　(Calculated in wind Load calculation)
　　Ft = Wind Force towards Transverse direction per saddle 5928 N
　　　　(Calculated in wind Load calculation)
　　FL' = Seismic Force towards longiudinal direction 18352.1 N
　　　　(Calculated in Seismic Load calculation)
　　Ft' = Seismic Force towards Transverse direction per saddle 9176.05 N

Saddle Reaction Force due to Wind in Transverse Direction Ft, [Fwt]: [As Per Dennis Moss, Page No. 260]
　　Fwt = 3 * Ft * B / E = 3 x 5928 x 2200 / 4370 = 8953.043 N
Saddle Reaction Force due to Wind in Longitudinal Direction FL, [FwL]: [As Per Dennis Moss, Page No. 260]
　　FwL = Max (FL , FL1, FL2, Fp) * B / Ls
　　FwL = Max (4710, N.R, 147072.89, N.R) * 2200 / 8953 = 36139.882 N
Saddle Reaction Force due to Earthquake or Friction Longitudinal Direction FL' , [FsL]
　　FsL = Max (FL' , FL1, FL2, Fp) * B / Ls
　　FsL = Max (18352.1, N.R, 147072.89, N.R ) * 2200 / 8953 = 36139.882 N
Saddle Reaction Force due to Earthquake in Transverse Direction Ft, [Fst]
　　Fst = 3 * Ft' * B / E = 3 x 9176.05 x 2200 / 4370 = 13858.565 N

LOAD COMBINATION RESULTS FOR Q : [As Per Dennis Moss, Page No. 260]
　　Longitudinal, Q1
　　Q1 = Wo / n + Max (FwL , FsL)
　　Q1 = 2451214.9 / 2 + Max (36139.882, 36139.882 ) = 1261747.327 N

　　Transverse, Q2
　　Q2 = Wo / 2 + Max (Fwt , Fst)
　　Q2 = 2451214.9 + Max (8953.043, 13858.565 ) = 1239466.01 N

　　Now,
　　Q = Mx of Q1 and Q2 = Max ( 1261747.327, 1239466.01 ) = 1261747.327 N
　　Where, A ≤ 0.25L = 800 ≤ 3313.25 Distance A is acceptable

HORIZONTAL VESSEL ANALYSIS
Wear Plate is Welded to the Shell, k = 0.1 [As Per ASME Section VII, Div. 2, Clause 4.15.6]
Stress Coefficients For Horizontal Vessels on Saddle Supports [As Per ASME Section VII, Div. 2, Table 4.15.1]
[Table 1] Value of Constant K [ASME Section VII, Div. 2, Fig 4.15.5, and Table 4.15.1]

Contact Angle (θ, deg)	K1	K1'	K2	K3	K4	K5	K6	K7	K8	K9	K10
139	0.139285	0.245607	0.91152	0.60402	0.330211	0.69975	0.038548	0.009637	0.318112	0.242458	0.041452

The angles θ, Δ, α, β, and ρ are in radians in the saddle calculations
[As Per ASME Section VII, Div. 2, Fig 4.15.5, and Table 4.15.1]

Description	Formula	Symbol	Value rad	Value °(deg)
Saddle Contact angle,	θ = 139 °(deg)	θ =	2.426	θ = 139
	Δ = (π / 6) ＋ (5θ / 12)	Δ =	1.5344	Δ = 87.9167
	α = 0.95(π － θ/2)	α =	1.8322	α = 104.975
	β = π － (θ/2)	β =	1.9286	β = 110.5
	ρ = 88.163 °(deg)	ρ =	1.5387	ρ = 88.163

Saddle Contact angle,	θ =	139 Degree	2.426	Radian
	Δ =	(π / 6) + (5 θ / 12)	1.535	Radian
	α =	0.95 (π - θ/2)	1.833	Radian
	β =	( π - θ/2)	1.929	Radian
[As Per ASME Section VII, Div. 2, Table 4.15.1]	ρ =	90.143 Degree	1.573	Radian

Saddle Contact angle, θ = 139 Degree = 2.426 Radian
Δ = (π / 6) + (5 θ / 12) = 1.535 Radian
α = 1.833 Radian
β = 1.929 Radian
ρ = 90.143 Degree [As Per ASME Section VII, Div. 2, Table 4.15.1] 1.573 Radian

The angles Δ, θ, β, and ρ are in radians in the calculations.
(2007년도 판이 상태좋은 캡춰필요) ASME SEC. VIII-Div.2 Table 4.15.1 Stress Coefficients For Horizontal Vessels on Saddle Supports