2022년 3월 16일 최종 수정 함 시작시간 = [2024-12-05 00:59:19.0607]
Vessel Volume & Level Calculation (2021년 11월 7일 수정) HTML 특수문자 리스트 (√ √ √ π Ø ø ｍ²ｍ³ｍ⁴ ㄷ ＋－ × ÷ ± ± ≤ ≥ ℃ ▶ ㅊ
Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α ε ο ο υ γ
α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ σ τ υ φ χ ψ ω ι ι ι υ ι γ
√ax² + bx + c
출처 : http://kor.pe.kr/util/4/charmap2.htm

출처 : HTML에서 수식 표현하기

Orientation :	Design Code :	Material(MPa) 주의?/FONT> :	Vessel Diameter (D) (mm)	Design Liquid Level (DLL) (mm)	Vessel Length (T.L to T.L) (mm)	(USED) Head Thk. (tHead) (mm)	Sdaale 간 거리 (Lsaddle) (mm)	Calc!
Internal Pressure(Pi) (MPa)	External Pressure(Pe) (MPa) (F/V = 0.101325 MPa)	Allowable Stress(MPa) 주의 (Blank=재질에 따라 자동입력) S=(MPa), Sy= (MPa)	Specific Gravity (비중)	Joint Effciency	Corrosion Allowance(CA) (mm)	(USED) Cylinder Thk. (tCyl) (mm)	90% DLL = 0.8042*D = 10052.5 (mm)
Volume And Surface Area 계산방법 선택 (2:1 Ellipsoidal and 10% Dish Head)			For Bi-lobe(or Tri-lobe) Tank C.L to C.L (C) C = D/(1.8~1.5)사이	Factor 1.8 ~ 1.5	Volume To Dia.(Sphere) V = ｍ³	Sphere Dia. (D) : D = (6V/3.14)^1/3 D = 22500.0 mm*

A) For Spherical Tank

B) For Hemi-Spherical Head

C) For 2:1 Ellipsoidal Dish Head

D) For 10% Dish Head

1) Spherical Tank : 12500 mm

ASME VIII, Div. 1

No.

DLL

Nominal Capacity

Storage Capacity

Storage
Ratio

Surface Area

P=Pi＋Ps

tHead

tShell

No.

m³

(%)

m²

MPa

12500

10850

6250

1022.6539

973.9018

95.233

490.9

0.4786

0.0532

0.5318

9.64

Where,　90% Capacity DLL = 0.8042 × D = 10052.5 (mm), Vnom = π×D³/ 6 = 1022.6539 (m³)
　　　(공칭용량) Vnom = 1022.6539 (m³)
　　　(저장용량) Vsto = 973.9018 (m³)
　　　( 표면적 ) AREA = π×D²= 490.874 m²
　　

[Table 1] Strength Calculation
　Vessel Size(D) : 12500 mm
　Where, 90% Capacity DLL = 0.8042 × D = 10053 (mm)
o (내압에 의한 필요두께의 계산) Required Thickness Calculation [Div.1]
　Vessel Material : SA553-Type.1
　Allowable Stress, S = 187.0 MPa, ASME SEC. II Part D, [TABLE 1A]
　Total Pressure, P = Pi ＋ Ps = 0.5318 MPa ( Pi=0.4786 MPa, Ps=0.0532 MPa, Ps:Static Head )
　Weld Joint Effciency, E = 1
　Tank Type : Spherical Shell
　t_Equator = Peq×R / ( 2SE - 0.2×Peq ) ＋ CA(0.75) = 9.13 mm, Peq = 0.5012 MPa
　t_Bottom = P×R / ( 2SE - 0.2P ) ＋ CA(0.75) = 9.64 mm, P = 0.5318 MPa
o (전체 표면적) AREA = π×D²= 490.874 m²

o 두께 Check : , Therefore, tDesign Thick. < Used Thick. OK
　Assumed Vessel Weight = 61.654 Ton (Sphere Shell Thick, 16.0 mm)

o Design External Pressure of Spherical Shell:
　 Material : SA553-Type.1, Ro = Ri ＋ headThk - CA = 6265.25 mm, tc= 15.25 mm
　 Factor A for Spherical Shells or Head UG-28(d) Factor A = 0.125 / ( Ro / tc ) = 0.00030426
　 Factor A for Spherical Shells or Head UG-28(d) Factor A = 0.125 / ( 6265.25 / 15.25) = 0.00030426
　 From ASME SEC. II Part D Fig. CS-3 Curve [Metric] B = 30.4258 MPa
　 Allowable External Pressure Pa = B / ( Ro / tc ) = 0.07406 MPa
　o Buckling Check of Head Plate, Pe(0.045) < Pa(0.0741) MPa. OK

1) Cylindrical Tank : 12500(D) × 22230(TL) × 34730(L) mm

ASME VIII, Div. 1

No.

DLL

Nominal Capacity

Storage Capacity

Storage
Ratio

Surface Area

P=Pi＋Ps

tHead

tShell

No.

m³

(%)

m²

MPa

12500

10850

6250

3750.6853

3488.8420

93.019

1363.8

0.4786

0.0532

0.5318

9.64

18.55

Where,　R = 0.5×D,　　Vnom = π×[(D³/ 6) ＋ (D²× L / 4)] = 3750.6853 (m³)
　　　(공칭용량) Vnom = Cylinder ＋ Both Heads = 2728.0314 ＋ 1022.6539 = 3750.6853 (m³)
　　　(저장용량) Vsto = Cylinder ＋ Both Heads = 2514.9401 ＋ 973.9018 = 3488.8420 (m³)
　　　( 표면적 ) AREA = π×D²＋ π×D×L = (Both Head: 490.874) ＋ (Cylinder: 872.97) = 1363.844 m²
　　

[Table 2] Strength Calculation
　Vessel Size : 12500(D) × 22230(TL) × 34730(L) mm
　Where, R = 0.5×D= 6250.0 mm
o (내압에 의한 필요두께의 계산) Required Thickness Calculation [Div.1]
　Vessel Material : SA553-Type.1
　Allowable Stress, S = 187.0 MPa, ASME SEC. II Part D, [TABLE 1A]
　Total Pressure, P = Pi ＋ Ps = 0.5318 MPa ( Pi=0.4786 MPa, Ps=0.0532 MPa, Ps:Static Head )
　Weld Joint Effciency, E = 1
　Head Type : Hemi-Spherical Head
　tHead_Btm = P×R / ( 2SE - 0.2P ) ＋ CA(0.75) = 9.64 mm, ( tHead_Top=9.13 mm),
　tCyl_Btm = P×R / ( SE - 0.6P ) ＋ CA(0.75) = 18.55 mm, ( tCyl_Top=17.53 mm)
o (전체 표면적) AREA = π×D²＋π×D×L = (Both Head: 490.874) ＋ (Cylinder: 872.97) = 1363.844 m²

o 두께 Check : , tDesign Thick. > Used Thick. NG. (사용두께를 키우세요)
　1) Both Head Weight = 61.654 Ton (Head Thick = 16.0 mm)
　2) Cylinder Weight = 109.645 Ton (Cylinder Thick = 16.0 mm)
　　Assumed Total Weight = 171.299 Ton

o Design External Pressure of Hemi-spherical Head:
　 Material : SA553-Type.1, Ro = Ri ＋ headThk - CA = 6265.25 mm, tc= 15.25 mm
　 Factor A for Spherical Shells or Head UG-28(d) Factor A = 0.125 / ( Ro / tc ) = 0.00030426
　 Factor A for Spherical Shells or Head UG-28(d) Factor A = 0.125 / ( 6265.25 / 15.25) = 0.00030426
　 From ASME SEC. II Part D Fig. CS-3 Curve [Metric] B = 30.4258 MPa
　 Allowable External Pressure Pa = B / ( Ro / tc ) = 0.07406 MPa
　o Buckling Check of Head Plate, Pe(0.045) < Pa(0.0741) MPa. OK

1) Cylindrical Tank : 12500(D) × 22230(TL) × 28480(L) mm

ASME VIII, Div. 1

No.

DLL

Nominal Capacity

Storage Capacity

Storage
Ratio

Surface Area

P=Pi＋Ps

tHead

tShell

No.

m³

(%)

m²

MPa

12500

10850

3125

11306.25

2159.3

3239.3584

3001.8911

92.669

1211.7

0.4786

0.0532

0.5318

18.53

18.55

Where,　R = 0.9045×D,　r = 0.172744×D,　z = 0.25×D,　Vnom = (π×D³/12) ＋ (L×π×D²/4) = 3239.3584 (m³)
　　　(공칭용량) Vnom = Cylinder ＋ Both Heads = 2728.0314 ＋ 511.3269 = 3239.3584 (m³)
　　　(저장용량) Vsto = Cylinder ＋ Both Heads = 2514.9401 ＋ 486.9509 = 3001.8911 (m³)
　　　( 표면적 ) AREA = 2×1.083849×D²＋π×D×L = (Both Head: 338.703) ＋ (Cylinder: 872.97) = 1211.673 m²
　　　( 표면적 공식 출처 : 일본 ) 바로가기

[Table 3] Strength Calculation
　Vessel Size : 12500(D) × 22230(TL) × 28480(L) mm
　Where, z = 0.25×D= 3125.0 mm,　 L = 0.9045×D= 11306.3 mm,　r =0.172744×D= 2159.3 mm,　C = 0.5
o (내압에 의한 필요두께의 계산) Required Thickness Calculation [Div.1]
　Vessel Material : SA553-Type.1
　Allowable Stress, S = 187.0 MPa, ASME SEC. II Part D, [TABLE 1A]
　Total Pressure, P = Pi ＋ Ps = 0.5318 MPa ( Pi=0.4786 MPa, Ps=0.0532 MPa, Ps:Static Head )
　Weld Joint Effciency, E = 1
　Head Type : 2:1 Ellipsoidal, [UG-32(c)] For t/R ≥ 0.002, tMin = 0.002×R = 23.36 mm > 16.0 mm tUsed NG!
　tHead_Btm = P×D×K / ( 2SE - 0.2P ) ＋ CA = 18.53 mm, ( tHead_Top=17.5 mm), K=1,
　tCyl_Btm = P×R / ( SE - 0.6P ) ＋ CA = 18.55 mm, ( tCyl_Top=17.53 mm)
o (전체 표면적) AREA = 2×1.083849×D²＋π×D×L = (Both Head: 338.703) ＋ (Cylinder: 872.97) = 1211.673 m²

o 두께 Check : , tDesign Thick. > Used Thick. NG. (사용두께를 키우세요)
　1) Both Head Weight = 42.541 Ton (Head Thick = 16.0 mm)
　2) Cylinder Weight = 109.645 Ton (Cylinder Thick = 16.0 mm)
　　Assumed Total Weight = 152.186 Ton

o Design External Pressure of 2:1 Ellipsoidal-Head:
　 Material : SA553-Type.1, Ro = 0.9×D ＋ headThk-CA = 11265.25 mm, tc= 15.25 mm
　 Factor A for Spherical Shells or Head UG-28(d) Factor A = 0.125 / ( 11265.25 / 15.25)
　 Factor A for Spherical Shells or Head UG-28(d) Factor A = 0.125 / ( Ro / tc ) = 0.00016922
　 From ASME SEC. II Part D Fig. CS-3 Curve [Metric] B = 16.9215 MPa
　 Allowable External Pressure Pa = B / ( Ro / tc ) = 0.02291 MPa
　o Buckling Check of Head Plate, Pe(0.045) > Pa(0.0229) MPa. NG

1) Cylindrical Tank : 12500(D) × 22230(TL) × 27074.36(L) mm

ASME VIII, Div. 1

No.

DLL

Nominal Capacity

Storage Capacity

Storage
Ratio

Surface Area

P=Pi＋Ps

tHead

tShell

No.

m³

(%)

m²

MPa

12500

10850

2422.18

12500

1250

3114.6174

2883.0968

92.567

1193.7

0.4786

0.0532

0.5318

28.14

18.55

Where,　L = 1.0×D,　r = 0.1×D,　z=0.193774×D,　C=0.3780223,　Vnom = (2×C×π×D³/12) ＋ (L×π×D²/4) = 3114.6174 (m³)
　　　(공칭용량) Vnom = Cylinder ＋ Both Heads = 2728.0314 ＋ 386.5860 = 3114.6174 (m³)
　　　(저장용량) Vsto = Cylinder ＋ Both Heads = 2514.9401 ＋ 368.1566 = 2883.0968 (m³)
　　　( 표면적 ) AREA = 2×1.0264×D²＋π×D×L = (Both Head: 320.75) ＋ (Cylinder: 872.97) = 1193.72 m²
　　　( 표면적 공식 출처 : 일본 ) 바로가기

[Table 4] Strength Calculation
　Vessel Size : 12500(D) × 22230(TL) × 27074.36(L) mm
　Where, z = 0.193774×D= 2422.18 mm,　 L = 1.0×D= 12500.0 mm,　r = 0.1×D= 1250.0 mm, 　C =0.3780223
o (내압에 의한 필요두께의 계산) Required Thickness Calculation [Div.1]
　Vessel Material : SA553-Type.1
　Allowable Stress, S = 187.0 MPa, ASME SEC. II Part D, [TABLE 1A]
　Total Pressure, P = Pi ＋ Ps = 0.5318 MPa ( Pi=0.4786 MPa, Ps=0.0532 MPa, Ps:Static Head )
　Weld Joint Effciency, E = 1
　Head Type : 10% Dish Head ( ASME SEC. VIII Div. Appendix 1.(d) for torispherical Head )
　tHead = P×L×M / ( 2SE - 0.2P ) ＋ CA = 28.14 mm, ( tHead_Top=26.56 mm), L=1.0×D=12500 mm, M=1/4×[3＋(L/r)^0.5] = 1.54057,
　tCyl = P×R / ( SE - 0.6P ) ＋ CA = 18.55 mm, ( tCyl_Top=17.53 mm)
o (전체 표면적) AREA = 2.0528×D²＋π×D×L = (Both Head: 320.75) ＋ (Cylinder: 872.97) = 1193.72 m²

o 두께 Check : , tDesign Thick. > Used Thick. NG. (사용두께를 키우세요)
　1) Both Head Weight = 40.286 Ton (Head Thick = 16.0 mm)
　2) Cylinder Weight = 109.645 Ton (Cylinder Thick = 16.0 mm)
　　Assumed Total Weight = 149.931 Ton
1
2
3
4
5
6
7
8

Material Selection for IMO TYPE "C" TANK Unit : MPa
MATERIAL	Weld Metal(용접봉강도)			Allowable Membrane Stress(f) 선급KR/LR
MATERIAL	Tensile Rm (=St)	Yield Re (=Sy)	Div.1 S	f = Min(Re/A, Rm/1.5)	f (Mpa)	A
A1106(Hign Mn)	660	400	N/A	f = Min(660/3.5, 400/1.5)	188.6	3.5
A553-TYPE1	640	420	187.0	f = Min(640/3.0, 420/1.5)	213.3	3.0
LT-FH32	440~570	315	N/A	f = Min(440/3.0, 315/1.5)	146.67
LT-FH36-TM	490~630	355	N/A	f = Min(490/3.0, 355/1.5)	163.33
SA240-304	515	205	138	f = Min(515/3.5, 205/1.5)	136.66	3.5
SA240-304L	485	170	115	f = Min(485/3.5, 170/1.5)	113.33
SA240-316	515	205	138	f = Min(515/3.5, 205/1.5)	136.66
SA240-316L	485	170	115	f = Min(485/3.5, 170/1.5)	113.33
SA516-60	410	215	118	ASME SEC. VIII Div.1 Allowable Stress
SA516-70	485	260	138
SA537-CL1	485	345	138
SA537-CL2	550	415	158

ASME SEC. VIII [Div. 1 WORK] ASME SEC. II PART D Table 1A [SI Unit] [CIS Calc]
No.	MATERIAL	Shell Allowbale Thick.	Min. Tensile Strength	Min. Yield Strength	Allowable Stress Sd (MPa)				Min. Yield Strength for Hydrostatic-Test	External Pressure (CS-Chart No)	..
No.	MATERIAL	t (mm)	St (MPa)	Sy (MPa)	40ºC	65ºC	100ºC	125ºC	Syt (MPa)	CS	..
1	SA516-55		380	205	108				184.5	CS-1
2	SA516-60		415	220	118				198	CS-2
3	SA516-65		450	240	128				216	CS-2
4	SA516-70		485	260	138				234	CS-2
5	SA537-CL1	t ≤ 64t	485	345	138	138	138	137	310.5	CS-4
6	SA537-CL1	64 < t ≤ 100	450	310	128				279	CS-4
7	SA537-CL2	t ≤ 64t	550	415	158	158	158	157	373.5	CS-4
8	SA537-CL2	64 < t ≤ 100	515	380	148	148	147	147	342	CS-4
9	SA537-CL2	100 < t ≤ 150	485	315	138	138	138	137	283.5	CS-4
10	SA36		400	250	114				225	CS-2
11	SA285-B	≤50t	345	185	98.6				166.5	CS-2
12	SA285-C	≤50t	380	205	108				184.5
13	SA240-304	G5	515	205	138	138	137	134	184.5	HA-1
14	SA240-304L	G5	485	170	115				153	HA-3
15	SA240-316	G5	515	205	138				184.5	HA-2
16	SA240-316L	G5	485	170	115				153	HA-4
17	SA553-TYPE1	W5	690	585	187	187	173	169	526.5	CS-3

ASME SEC. VIII [Div. 2 - Class 2 WORK] ASME SEC. II PART D Table 5A [SI Unit]
No.	MATERIAL	Shell Allowbale Thick.	Min. Tensile Strength	Min. Yield Strength	Allowable Stress Sd (MPa)				Min. Yield Strength for Hydrostatic-Test	External Pressure (CS-Chart No)	..
No.	MATERIAL	t (mm)	St (MPa)	Sy (MPa)	40ºC	65ºC	100ºC	125ºC	Syt (MPa)	CS	..
1	SA516-55		380	205	138	130	126	124	194.75
2	SA516-60		415	220	147	138	134	132	209
3	SA516-65		450	240	161	151	147	144	228
4	SA516-70		485	260	175	164	159	157	247
5	SA537-CL1	t ≤ 64t	485	345	201				327.75
6	SA537-CL1	64 < t ≤ 100	450	310	187	187	181	174	294.5
7	SA537-CL2	t ≤ 64t	550	415	230				394.25
8	SA537-CL2	64 < t ≤ 100	515	380	215				361
9	SA537-CL2	100 < t ≤ 150	485	315	201	196	185	178	299.25
10	SA36		400	250	165	156	151	148	237.5
11	SA285-B	t ≤ 50t	345	185	124	117	113	111	175.75
12	SA285-C	t ≤ 50t	380	205	138	130	126	124	194.75
13	SA240-304		515	205	138				194.75
14	SA240-304L		485	170	115				161.5
15	SA240-316		515	205	138				194.75
16	SA240-316L		485	170	115				161.5
17	SA553-TYPE1	t ≤ 150	690	585	273				555.75	W4

SHELL BUCKLING CHECK [GL RULES]
출처 : ASME External Pressure, 링크 : Design https://www.pveng.com/home/asme-code-design/external-pressure-methods/
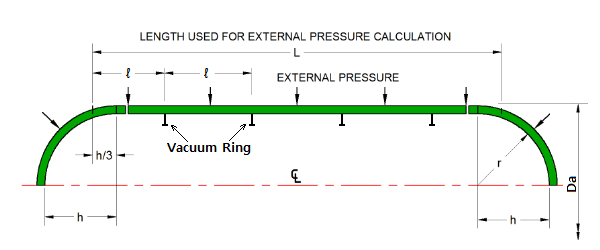
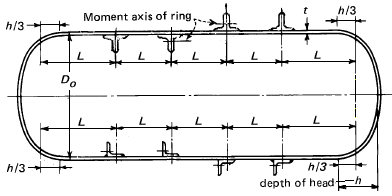
2 Designing for External Pressure
The easiest way to design for external pressure is to make the shell thick enough to make the vessel stable with an acceptable factor of
safety (pass code calculations). The length of the vessel used in the calculations includes some of the head at each end.
The calculations are found in ASME VIII-1 UG-28. The shell calculations are for a cylinder with supported ends
(the heads at each end). Calculations are also given for the heads which are treated as spheres.

Data Input :
출처 : Germanischer Lloyd (GL) RULE, External Pressure, 링크 : (크로아티아) BILOBE_실린더_계산_논문_620084.Senjanovic_Structure_design.pdf
출처 : Germanischer Lloyd (GL) RULE, External Pressure, 링크 : 003_STRUCTURE DESIGN OF CARGO TANKS IN RIVER LIQUEFIED GAS CARRIERS　ds36_126.pdf

Head Type	headType =
Design External Pressure	Pe =	0.45	bar	Full Vacuum F.V= 1.01325 bar
Outside diameter ( Cylinder )	Da =	4730	mm
(Assumed) Shell Plate Thickness	t =	13.08	mm
Allowance for corrosion and wear	c =	0	mm
Vacuum Ring pitch(ℓ), Or Length of shell(L)	ℓ =	3722	mm
Modulus of elasticity at design temperature	Et =	206000	N/mm²	SA203-304(L), SA203-316(L) : 193,000 N/mm², Carbon and 9% Nickel : 206,000 N/mm², High Mn. : 175,000 N/mm²
Poisson's ratio	υ =	0.3
integral number of waves; nw = 1.63 * [(Da/ℓ)² * Da/tc]^0.25 where, n > 2 and n > z	nw =	8.01		DNV-GL 7.1.3 91쪽
z = 3.141592 * Da / ( 2*ℓ )	z =	1.9962
Shell Thick. to Out-Diameter Ratio	(t-c) / Da =	0.0027643
Safety factor against elastic buckling, Sk = 3 + [0.002 / (tc/R)]	Sk =	3.3618
Vacuum Ring Size, Ex)H400x200x20x10 OR H400x20+300x10	SIZE =			ex) T400x20+200x10 or FB100x6
SUBMIT

3. ASME SEC. VIII Div. 1 설계외압에 의한 Vacuum Ring 시뮬레이션
　[Alternate] Design External Pressure Check by ABS (ASME SEC.VIII Division 1 Rule )

1. Hemi-Spherical Head :

MATL =

SA553-Type.1

Design External Pressure

Pe =

0.045

MPa

Elastic modulus

Et =

206000

MPa

Hemi-Spherical Head Long Radius, Ro = Do / 2

Ro =

2365.0

Head Plate Thickness,

th =

16.0

Corrosion Allowance

CA =

0.0

Corroded Thickness

t = th-CA

16.0

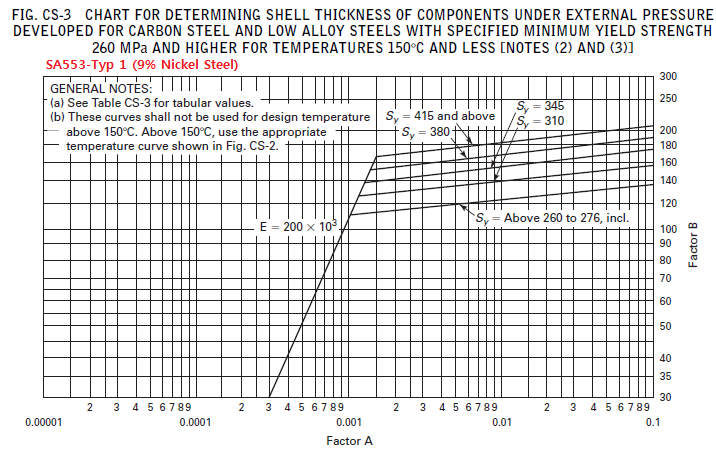
Factor A for Head plate A = 0.125 / ( Ro / tc)

FACTOR A =

0.0008457

Factor B from ASME SEC. II Part D Fig. CS-3 Curve [Metric]

FACTOR B =

84.56660

MPa

[UG－28 ]Step 4.] Allowable External Pressure, Pa =
B
(Ro/t)

Pa =

0.57212
572.12

MPa
kPa

Buckling Check of Cylinder Shell Plate,

Pe(0.045) < Pa(0.57212) MPa

2. Shell plate :

MATL =

SA553-Type.1

Design External Pressure,

Pe =

0.045

MPa

Elastic modulus

Et =

206000

MPa

Outside Diameter

Do =

4730.0

Stiffener pitch

L =

3722.0

Recommend Stiffener pitch (추천 Picth by Bob-LONG for API 620 Tank)

Ls =

11409.1

(Assumed) Shell Plate Thickness

ts =

13.075

Corrosion Allowance

CA =

0.0

Corroded Thickness

t = ts-CA

13.075

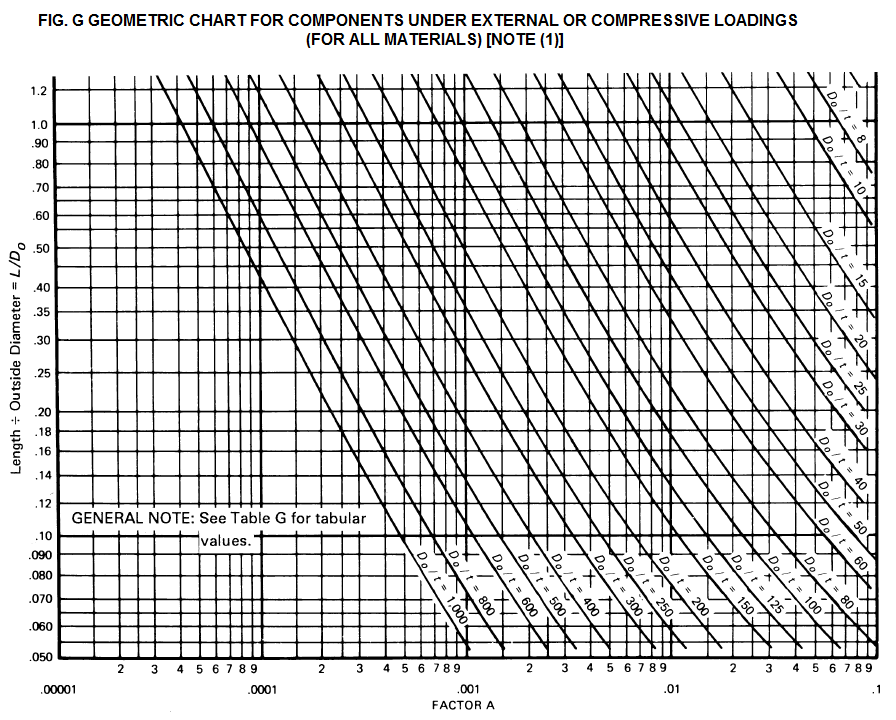
Stiffener pitch to Diameter Ratio, L/Do > 0.055, OK! [Step 1 from FIG. G]

L / Do =

0.7869

Ref. FIG. G

Out-Diameter to thickness ratio, Do/tc < 1000, OK! [Step 2 from FIG. G]

Do / t =

361.7591

Ref. FIG. G

Factor A for Cylinderical Shells form ASME SEC II, Part D, FIG-G.

FACTOR A =

0.0002550

Ref. FIG. G

Factor B from ASME SEC. II Part D Fig. CS-3 Curve [Metric]

FACTOR B =

25.49597

MPa

[UG－28 (c) Step 6] Allowable External Pressure, Pa =
4 · B
3 · (Do/t)

Pa =

0.09397
93.97

MPa
kPa

Buckling Check of Cylinder Shell Plate, ASME VIII, Div 1

Pe(0.045) < Pa(0.09397) MPa
Pe(0.45) < Pa(0.9397) bar.g

[미국 수소법 CGA_H3] Pc = [2.6×Et×(tc/Da)^2.5] / [(L/Da) - 0.45×(tc/Da)^0.5]

Pc =

0.2819

MPa

[minL 역계산] minL = [(2.6×Et×(tc/Da)^2.5) / Pc + 0.45×(tc/Da)^0.5] × D

minL =

3722

Buckling Check of Cylinder Shell Plate, by CGA H-3 Rules
Pe = Safety Factor 2 ⋅ F/V = 2.0265 bar.g

Pe(0.2027) < Pc(0.2819) MPa
Pe(2.027) < Pc(2.819) bar.g

3. Stiffener Ring ( Vacuum Ring ) :

MATL =

SA553-Type.1

Stiffener Ring Size

Size =

T400x20+200x10

Section Area of Stiffener Ring

As =

cm²

　[UG-29 Step 1.] B = 3/4 ⋅ Pe ⋅ Do / (t+As/Ls)

B =

10.1628

MPa

　[UG-29 Step 5.] A = 2 ⋅ B / Et

A =

0.0000987

　[UG-29(a)] Required moment of inertia of the combined ring-shell cross section
　　　　　Is' = Do² ⋅ Ls(t+As/Ls) ⋅ A / 10.9 ⋅ [mm⁴]
　　　　　Is' = 4730² ⋅ 3722 ⋅ (13.075+9800/3722) ⋅ 0.0000987 / 10.9 [mm⁴]

Is' =

1184.05

cm⁴

　[UG-29(a)] available moment of inertia of combined ring-shell cross section
　　　　　　　　 See. Bellow Table

I' =

34554.58

cm⁴

　Check of inertia cross section, Is' / I' < 1.0 OK

Is' / I' =

0.0343 < 1.0 OK

Available moment of inertia calculation (I') : 　　　　Stiffener Size : T400x20+200x10

No.	b	d	A=b ⋅ d	y	A ⋅ y	h = y-C1	Ah²	Ig=b ⋅ d³/12	SKETCH
No.	cm	cm	cm²	cm	cm³	(cm)	cm⁴	cm⁴
3	20.0	1.0	20.0	41.025	820.5	23.58	11125.04	1.67
2	2.0	39.0	78.0	21.025	1639.95	3.58	1002.47	9886.5
Shell	29.54	1.525	45.05	0.7625	34.35	-16.68	12530.16	8.73
	SUM	∑ =	143.05		2494.8		24657.68	9896.9

C1	= ∑(AY) / ∑(A) (무게중심 위치)	C1 =	17.44	cm	무게중심에서 FLANGE 하단 까지 떨어진 거리
C2	= H - C1	C2 =	24.085	cm	무게중심에서 FLANGE 상단 까지 떨어진 거리
∑(A)	= Sum of Section Area (단면적)	∑(A)=	143.05	cm²	단면적 (빗금전체)
Ix	= ∑(Ah²) + ∑(Ig)	Ix =	34554.58	cm⁴	X축 단면2차모멘트 (Moment of inertia)
Zx	= Ix / Max(C1, C2)	Zx =	1434.69	cm³	X축 단면계수 (Section Modulus)
Zmax	= Ix / Min(C1, C2)	Zmax =	1981.34	cm³	X축 (최대) 단면계수
Rx	= SQRT( Ix / A )	Rx =	15.54	cm	X축 회전반경
Ry	= SQRT( Iy / A )	Ry =	5.27	cm	Y축 회전반경
Section Area(Shell 포함)		Sarea =	143.05	cm²	Section Area(Shell 포함)
Ring 단면적 (Shell 제외)		ARing =	98	cm²	Ring 단면적 (Shell 제외)
Ring 원주길이		Leng =	6.23	m	Ring 길이(m) = 3.141592×(Di-C1)
Ring 단위중량 (kg/m),		WTm =	76.93	kg/m	단위중량(kg/m)
Ring Weight, Shell(1) 제외 중량		WT =	479.2	kg	Ring 1 PCS 중량(kg)

4. ASME SEC. VIII Div. 2 설계외압에 의한 Vacuum Ring 시뮬레이션
　[Alternate] Design External Pressure Check by ABS (ASME SEC.VIII Division 2 Rule )
A. Spherical Shell or Hemi-Head Required Thickness: Div.2 EQ.4.4.2, EQ.4.4.7

1. Spherical Shell or Hemi-Spherical Head :	MATL =	SA553-Type.1
Design External Pressure,	Pe =	0.045	MPa
Elastic modulus	Et =	206000	MPa
Minimum Specified Yield Strength at Design Temperature(80℃)	Sy =	400.0	MPa
Hemi-Spherical Head Long Radius, Ro = Do / 2	Ro =	2365.0	mm
Head Plate Nominal Thickness,	th =	16.0	mm
Head Plate Corrosion Allowance	CA =	0.0	mm
Head Plate Corroded Thickness	t = th-CA	16.0	mm
Predicted Elastic buckling stress, Fhe = 0.075 × Ey × [tc / Ro]　(Eqn. 4.4.53)	Fhe =	104.52	MPa
Safety Factor　　 If Fic ≤ 0.55×Sy then FS = 2.0 Eqn. 4.4.1)	FS =	2.000
If Fhe　≤ 0.55×Sy then Fha = Fhe / FS (Eqn. 4.4.57)	Fha =	52.26	MPa
Allowable External Pressure, Pa = FS × Fha × [t / Ro]　　　　(Eqn. 4.4.58)	Pa =	0.70714	MPa
Req'd Min. Head plate thickness for Ext. Pressure Tmin_EP = Ro × Pe / (FS × Fha) + CA	Tmin_EP =	1.02	mm
Check : Pe ≤ Pa OK, Tmin_EP ≤ t	Pe ≤ Pa	O.K

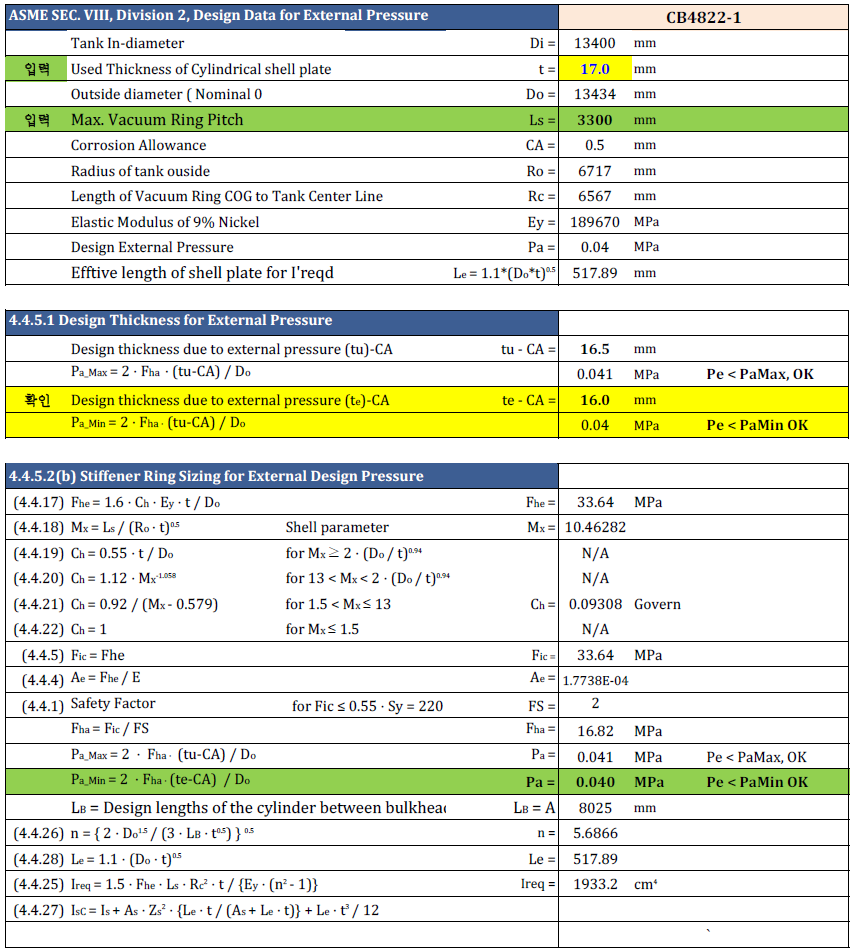
B. For Cylindrical Shell Required Thickness :

No.	t mm	Do mm	Fhe MPa	Mx	Ch	Fic MPa	Ae	FS	Fha MPa	Pe Mpa	< Pa OK MPa
1	10.0	4730	39.8156	15.4684	0.0618	39.81564	0.00019328	2.0000	19.9078	0.045	< 0.0779 OK

Sy =400.0 MPa, ttc =9.25 mm, Ro =2365.0 mm, Do =4730.0 mm, Do/t= 511.35 < 2000 OK,
Mx=[15.4684], Ch=[0.0618], Fhe=[39.8156], Fic=[39.8156], FS=[2.0]
Pe(0.045 MPa) < Pa_div2=[0.0779] Mpa , Pa_div2=[0.779] bar.g, OK
ASME SEC. VIII Div. 2 Examples : [파일 : (SB-Q21-0618_0628) 선보공업_2nd_견적_강도계산.xlsx]

1. Check by DNV-GL RULES, (설계외압에 의한 Vacuum Ring 시뮬레이션) 아래 Formula 변천사 출처
Case A ) 중요 : Safety Fctor Sk = 4, Max( 4, 3 + [ 0.002 / (t-c / R) ] )

n	GL Rules Pcr_GL (bar.g) Sk = 3.3618	DNV-GL RULES Pcr_DNV (bar.g) when, Sk = 4.0	Remark
4	9.1795	7.7148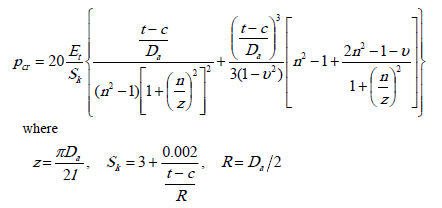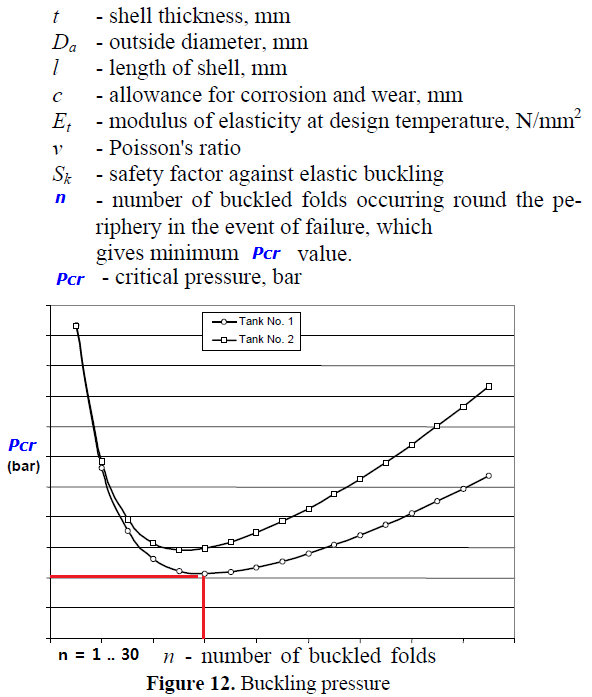
5	2.9590	2.4869
6	1.3600	1.1430
7	0.9233	0.7760
8	0.8525 (Sk = 3.3618)	0.7165 ( Sk = 4.0 ) Minimum Pcr( critical pressure ) bar.g
9	0.9231	0.7758
10	1.0612	0.8919
11	1.2393	1.0416
12	1.4463	1.2156
13	1.6773	1.4096
14	1.9297	1.6218
15	2.2026	1.8512
16	2.4953	2.0972
17	2.8074	2.3595
18	3.1388	2.6380
19	3.4893	2.9326
20	3.8589	3.2432
21	4.2476	3.5698
22	4.6552	3.9124
23	5.0819	4.2710
24	5.5275	4.6455
25	5.9921	5.0360
26	6.4757	5.4425
Where, Shell plate Material : SA553-Type.1 Vacuum Ring Pitch, L = [3722.0] mm, Buckling Coefficient, z = 3.141592 * Da / ( 2 * L ) = 1.9962 The critical pressure is found by an iteration process over the range n, where n > z. Buckling Safety factor, Sk = 3 + (0.002/(tc/Ro)) = 3.36176 n = 8 - number of buckled folds occurring round the periphery in the event of failure, which give minimum pcr value. Pcr = 0.8525 bar.g, Minimum Pcr value.
Evaluation : (평가결과) 　1. Design External Pressure : 0.45(bar) < Cretical External Pressure 0.8525(bar) 이므로 [안전]합니다. 　2. 안전율 [Pe/Pcr = 0.5278] 로써 OVER DESIGN 상태이므로 Shell 두께를 적정두께로 줄이시기를 추천 합니다.

2. Check by DNV-GL vs. ABS Rules (ASME SEC. VIII Div.1 설계외압에 의한 Vacuum Ring 시뮬레이션
Case B ) 중요 : Safety Fctor Sk = 3 + [0.002 / (t-c / R) ]

DNV-GL when, Sk = 3 + [0.002 / (t-c / R)				ABS Rules = ASME SEC. VIII Division 1 Do/t = 361.76 < 1000 이하 OK, L/Do = 0.78689, CA = 0 mm
t(mm)	Sk	nz	Pcr (bar)	t(mm)	Do / tc	Factor A	Factor B	Pa (bar)	Pcr/Pa
10	3.473	18.428	0.41993	10	473.000	0.00016676	16.676	0.4701	0.8933
10.5	3.45048	17.984	0.47797	10.5	450.476	0.00018029	18.029	0.5336	0.8957
Where, Shell Material : SA553-Type.1, Vacuum Ring Pitch L = [3722.0] mm, n = 18 , number of buckled folds occurring round the periphery in the event of failure, which give minimum pcr value. Pcr = 0.8525 bar.g, Minimum Pcr value.
Evaluation : (평가결과) 　1. Shell 두께 10.5 (mm) 일 경우, 　　 Design External Pressure : 0.45(bar) < Cretical External Pressure 0.4780(bar) 이므로 [안전]합니다. 　2. 안전율 [Pe/Pcr = 0.9415] 로써 OVER DESIGN 상태이므로 Shell 두께를 적정두께로 줄이시기를 추천 합니다.

필요한 단면 2차 모멘트 ( DNV-GL Rules)
DNVGL-RU-SHIP-Pt5Ch7 (2017) Liquefied gas tankers.pdf Pt5. Ch.7 Secction 22
2.4.1 2.4 Scantling due to external pressure

2.4.4 Stiffening rings
The requirements for scantling of stiffening rings are given in terms of minimum moment of inertia for the member, in mm⁴.

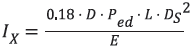
Ix = 0.18 * 4730 * 0.045 * 3722 * 4730²/ 206000 = 1.5487367E7 mm⁴= 1548.74 cm⁴

Where :
Ds = diameter to the neutral axis of stiffener in mm
Ped = external design pressure in MPa defined in [1.2.4].
Ls = 0.75 * SQRT(D*t)
The length of the shell in mm contributing to the moment of inertia is limited by
Stiffening rings shall extent completely around the circumference of the shell.

2.4.2) Hemi-Spherical Head for Allowable Compressive Stress
출처 : 002_IMO C형 독립탱크의 설계치수 계산과정 및 평가방법에 대한 고찰 7 쪽 Consideration for IMO Type C Independent Tank Rule Scantling Process and Evaluation Methods-1.pdf

The spherical shell shall be checked so that elastic instability or membrane yield does not occur.
The allowable design pressure shall be complied with the requirement in [2.8.2].
calculation of elastic instability
The pressure Pc, in bar.g, corresponding to elastic instability of a head plate,
shall be determined from the following formula:
Pc = 2.4 * E * [ (tHead-CA) /R ]² = 2.4 * 206000.0 * [(16.0 - 0.75) / 2365]² = 20.557 bar.g
Py = 20 * Fy * [(tHead-CA) / R ] = 20 * 400.0 * (16.0 - 0.75) / 2365) = 51.586 bar.g
Acceptance criteria for Head Plate :
　Pe(0.45) < Min(Pc / 3, Py/3 ) then OK
　Pe(0.45) < Min( 20.557/3, 　51.586/3 ) then OK
　Pe(0.45) < Min( 6.852, 　17.195 ) then OK

출처 : (크로아티아) BILOBE_실린더_계산_논문_620084.Senjanovic_Structure_design.pdf
8. SHELL BUCKLING ANALYSIS
8.1. CYLINDRICAL SHELL
In the case of a large external pressure a segment of
the cylindrical tank shell between the two vacuum rings
may lose stability. According to the GL Rules the critical
pressure for elastic buckling of a cylindrical shell is determined
by the following formula [5]

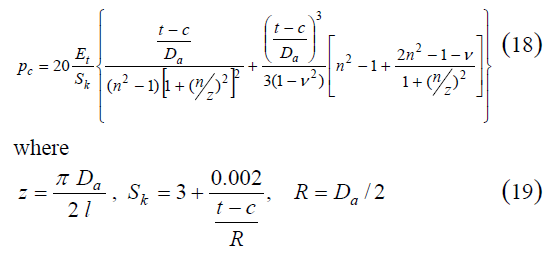
출처 : 003_STRUCTURE DESIGN OF CARGO TANKS IN RIVER LIQUEFIED GAS CARRIERS　ds36_126.pdf
4. Shell Buckling
4.1 Cylindrical shell
In the case of external pressure a segment of the cylindrical tank shell between the two vacuum rings
may lose stability. According to the GL Rules the critical pressure for elastic buckling of a cylindrical
shell is determined by the following formula [Rules GL 2000]:

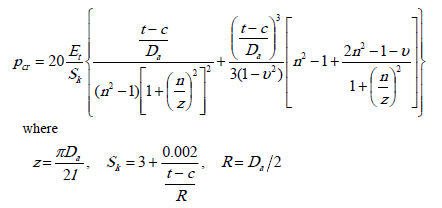
출처 DNV_GL : DNVGL-RU-SHIP-Pt4Ch7.pdf 91 쪽
Stiffener Size : T400x20+200x10　　　　Shell Section : t9 x 230 mm

No.	b	d	A=b*d	y	A*y	h = y-C1	Ah²	Ig=b*d³/12	SKETCH
No.	cm	cm	cm²	cm	cm³	(cm)	cm⁴	cm⁴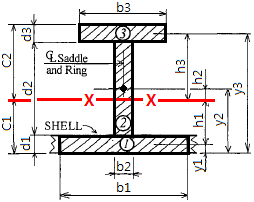
3	20.0	1.0	20.0	40.425	808.5	20.21	8167.27	1.67
2	2.0	39.0	78.0	20.425	1593.15	0.21	3.37	9886.5
Shell	23.01	0.925	21.28	0.4625	9.84	-19.75	8304.31	1.52
	SUM	∑ =	119.28		2411.49		16474.95	9889.68

C1	= ∑(AY) / ∑(A) (무게중심 위치)	C1 =	20.217	cm	무게중심에서 FLANGE 하단 까지 떨어진 거리
C2	= H - C1	C2 =	20.708	cm	무게중심에서 FLANGE 상단 까지 떨어진 거리
∑(A)	= Sum of Section Area (단면적)	∑(A)=	119.28	cm²	단면적 (빗금전체)
Ix	= ∑(Ah²) + ∑(Ig)	Ix =	26364.64	cm⁴	X축 단면2차모멘트 (Moment of inertia)
Zx	= Ix / Max(C1, C2)	Zx =	1273.16	cm³	X축 단면계수 (Section Modulus)
Zmax	= Ix / Min(C1, C2)	Zmax =	1304.08	cm³	X축 (최대) 단면계수
Rx	= SQRT( Ix / A )	Rx =	14.87	cm	X축 회전반경
Ry	= SQRT( Iy / A )	Ry =	3.7	cm	Y축 회전반경
Section Area(Shell 포함)		Sarea =	119.28	cm²	Section Area(Shell 포함)
Ring 단면적 (Shell 제외)		ARing =	98	cm²	Ring 단면적 (Shell 제외)
Ring 원주길이		Leng =	6.22	m	Ring 길이(m) = 3.141592×(Di-C1)
Ring 단위중량 (kg/m),		WTm =	76.93	kg/m	단위중량(kg/m)
Ring Weight, Shell(1) 제외 중량		WT =	478.5	kg	Ring 1 PCS 중량(kg)

Stiffener Size : FB 300x10　　　　Shell Section : t10 x 200 mm

No.	b	d	A=b*d	y	A*y	h = y-C1	Ah²	Ig=b*d³/12	SKETCH
No.	cm	cm	cm²	cm	cm³	(cm)	cm⁴	cm⁴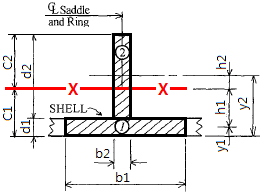
2	1.0	30.0	30.0	16.0	480	6.2	1153.2	2250
1	20.0	1.0	20.0	0.5	10	-9.3	1729.8	1.67
	SUM	∑ =	50		490		2883	2251.67

C1	= ∑(AY) / ∑(A) (무게중심 위치)	C1 =	9.8	cm	무게중심에서 FLANGE 하단 까지 떨어진 거리
C2	= H - C1	C2 =	21.2	cm	무게중심에서 FLANGE 상단 까지 떨어진 거리
∑(A)	= Sum of Section Area (단면적)	∑(A)=	50.00	cm²	단면적 (빗금전체)
Ix	= ∑(Ah²) + ∑(Ig)	Ix =	5134.67	cm⁴	X축 단면2차모멘트 (Moment of inertia)
Zx	= Ix / Max(C1, C2)	Zx =	242.2	cm³	X축 단면계수 (Section Modulus)
Zmax	= Ix / Min(C1, C2)	Zmax =	523.95	cm³	X축 (최대) 단면계수
Rx	= SQRT( Ix / A )	Rx =	10.13	cm	X축 회전반경
Ry	= SQRT( Iy / A )	Ry =	3.66	cm	Y축 회전반경
Section Area(Shell 포함)		Sarea =	50	cm²	Section Area(Shell 포함)
Ring 단면적 (Shell 제외)		ARing =	30	cm²	Ring 단면적 (Shell 제외)
Ring 원주길이		Leng =	6.25	m	Ring 길이(m) = 3.141592×(Di-C1)
Ring 단위중량 (kg/m),		WTm =	23.55	kg/m	단위중량(kg/m)
Ring Weight, Shell(1) 제외 중량		WT =	147.2	kg	Ring 1 PCS 중량(kg)

Stiffener Size : T 400x20+150x10　　　　Shell Section : t15 x 200 mm

No.	b	d	A=b*d	y	A*y	h = y-C1	Ah²	Ig=b*d³/12	SKETCH
No.	cm	cm	cm²	cm	cm³	(cm)	cm⁴	cm⁴
3	15.0	1.0	15.0	41.0	615	22.5	7593.75	1.25
2	2.0	39.0	78.0	21.0	1638	2.5	487.5	9886.5
Shell	20.0	1.5	30.0	0.75	22.5	-17.75	9451.88	5.63
	SUM	∑ =	123		2275.5		17533.13	9893.38

C1	= ∑(AY) / ∑(A) (무게중심 위치)	C1 =	18.5	cm	무게중심에서 FLANGE 하단 까지 떨어진 거리
C2	= H - C1	C2 =	23.0	cm	무게중심에서 FLANGE 상단 까지 떨어진 거리
∑(A)	= Sum of Section Area (단면적)	∑(A)=	123.00	cm²	단면적 (빗금전체)
Ix	= ∑(Ah²) + ∑(Ig)	Ix =	27426.5	cm⁴	X축 단면2차모멘트 (Moment of inertia)
Zx	= Ix / Max(C1, C2)	Zx =	1192.46	cm³	X축 단면계수 (Section Modulus)
Zmax	= Ix / Min(C1, C2)	Zmax =	1482.51	cm³	X축 (최대) 단면계수
Rx	= SQRT( Ix / A )	Rx =	14.93	cm	X축 회전반경
Ry	= SQRT( Iy / A )	Ry =	3.26	cm	Y축 회전반경
Section Area(Shell 포함)		Sarea =	123	cm²	Section Area(Shell 포함)
Ring 단면적 (Shell 제외)		ARing =	93	cm²	Ring 단면적 (Shell 제외)
Ring 원주길이		Leng =	6.23	m	Ring 길이(m) = 3.141592×(Di-C1)
Ring 단위중량 (kg/m),		WTm =	73.01	kg/m	단위중량(kg/m)
Ring Weight, Shell(1) 제외 중량		WT =	454.5	kg	Ring 1 PCS 중량(kg)

Stiffener Size : H 200 * 20 + 100 x 10　　　　Shell Section : t20 x 150 mm

No.	b	d	A=b*d	y	A*y	h = y-C1	Ah²	Ig=b*d³/12	SKETCH
No.	cm	cm	cm²	cm	cm³	(cm)	cm⁴	cm⁴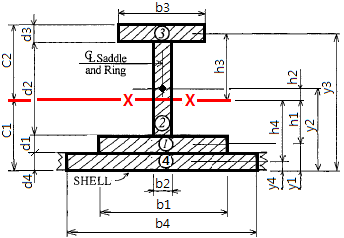
3	10.0	2.0	20.0	22.0	440	13.47	3626.66	6.67
2	1.0	17.0	17.0	12.5	212.5	3.97	267.4	409.42
1	10.0	2.0	20.0	3.0	60	-5.53	612.5	6.67
Shell	15.0	2.0	30.0	1.0	30	-7.53	1702.83	10
	SUM	∑ =	87		742.5		6209.4	432.75

C1	= ∑(AY) / ∑(A) (무게중심 위치)	C1 =	8.534	cm	무게중심에서 FLANGE 하단 까지 떨어진 거리
C2	= H - C1	C2 =	14.466	cm	무게중심에서 FLANGE 상단 까지 떨어진 거리
∑(A)	= Sum of Section Area (단면적)	∑(A)=	87.00	cm²	단면적 (빗금전체)
Ix	= ∑(Ah²) + ∑(Ig)	Ix =	6642.15	cm⁴	X축 단면2차모멘트 (Moment of inertia)
Zx	= Ix / Max(C1, C2)	Zx =	459.16	cm³	X축 단면계수 (Section Modulus)
Zmax	= Ix / Min(C1, C2)	Zmax =	778.32	cm³	X축 (최대) 단면계수
Rx	= SQRT( Ix / A )	Rx =	8.74	cm	X축 회전반경
Ry	= SQRT( Iy / A )	Ry =	3.21	cm	Y축 회전반경
Section Area(Shell 포함)		Sarea =	87	cm²	Section Area(Shell 포함)
Ring 단면적 (Shell 제외)		ARing =	57	cm²	Ring 단면적 (Shell 제외)
Ring 원주길이		Leng =	6.26	m	Ring 길이(m) = 3.141592×(Di-C1)
Ring 단위중량 (kg/m),		WTm =	44.75	kg/m	단위중량(kg/m)
Ring Weight, Shell(1) 제외 중량		WT =	279.9	kg	Ring 1 PCS 중량(kg)

Stiffener Size : HB 400x200x20/10　　　　Shell Section : t25 x 300 mm

No.	b	d	A=b*d	y	A*y	h = y-C1	Ah²	Ig=b*d³/12	SKETCH
No.	cm	cm	cm²	cm	cm³	(cm)	cm⁴	cm⁴
3	20.0	2.0	40.0	42.5	1700	28	31351.04	13.33
2	1.0	37.0	37.0	23.0	851	8.5	2670.73	4221.08
1	20.0	2.0	40.0	3.5	140	-11	4843.52	13.33
Shell	30.0	2.5	75.0	1.25	93.75	-13.25	13175.14	39.06
	SUM	∑ =	192		2784.75		52040.43	4286.81

C1	= ∑(AY) / ∑(A) (무게중심 위치)	C1 =	14.504	cm	무게중심에서 FLANGE 하단 까지 떨어진 거리
C2	= H - C1	C2 =	28.996	cm	무게중심에서 FLANGE 상단 까지 떨어진 거리
∑(A)	= Sum of Section Area (단면적)	∑(A)=	192.00	cm²	단면적 (빗금전체)
Ix	= ∑(Ah²) + ∑(Ig)	Ix =	56327.25	cm⁴	X축 단면2차모멘트 (Moment of inertia)
Zx	= Ix / Max(C1, C2)	Zx =	1942.59	cm³	X축 단면계수 (Section Modulus)
Zmax	= Ix / Min(C1, C2)	Zmax =	3883.57	cm³	X축 (최대) 단면계수
Rx	= SQRT( Ix / A )	Rx =	17.13	cm	X축 회전반경
Ry	= SQRT( Iy / A )	Ry =	6.57	cm	Y축 회전반경
Section Area(Shell 포함)		Sarea =	192	cm²	Section Area(Shell 포함)
Ring 단면적 (Shell 제외)		ARing =	117	cm²	Ring 단면적 (Shell 제외)
Ring 원주길이		Leng =	6.24	m	Ring 길이(m) = 3.141592×(Di-C1)
Ring 단위중량 (kg/m),		WTm =	91.85	kg/m	단위중량(kg/m)
Ring Weight, Shell(1) 제외 중량		WT =	572.9	kg	Ring 1 PCS 중량(kg)

Stiffener Size : H 500x200x20/10　　　　Shell Section : t30 x 400 mm

No.	b	d	A=b*d	y	A*y	h = y-C1	Ah²	Ig=b*d³/12	SKETCH
No.	cm	cm	cm²	cm	cm³	(cm)	cm⁴	cm⁴
3	20.0	2.0	40.0	53.0	2120	37.62	56601.55	13.33
2	1.0	47.0	47.0	28.5	1339.5	13.12	8086.62	8651.92
1	20.0	2.0	40.0	4.0	160	-11.38	5182.91	13.33
Shell	40.0	3.0	120.0	1.5	180	-13.88	23128.52	90
	SUM	∑ =	247		3799.5		92999.6	8768.58

C1	= ∑(AY) / ∑(A) (무게중심 위치)	C1 =	15.383	cm	무게중심에서 FLANGE 하단 까지 떨어진 거리
C2	= H - C1	C2 =	38.617	cm	무게중심에서 FLANGE 상단 까지 떨어진 거리
∑(A)	= Sum of Section Area (단면적)	∑(A)=	247.00	cm²	단면적 (빗금전체)
Ix	= ∑(Ah²) + ∑(Ig)	Ix =	101,768	cm⁴	X축 단면2차모멘트 (Moment of inertia)
Zx	= Ix / Max(C1, C2)	Zx =	2635.32	cm³	X축 단면계수 (Section Modulus)
Zmax	= Ix / Min(C1, C2)	Zmax =	6615.63	cm³	X축 (최대) 단면계수
Rx	= SQRT( Ix / A )	Rx =	20.3	cm	X축 회전반경
Ry	= SQRT( Iy / A )	Ry =	8.69	cm	Y축 회전반경
Section Area(Shell 포함)		Sarea =	247	cm²	Section Area(Shell 포함)
Ring 단면적 (Shell 제외)		ARing =	127	cm²	Ring 단면적 (Shell 제외)
Ring 원주길이		Leng =	6.23	m	Ring 길이(m) = 3.141592×(Di-C1)
Ring 단위중량 (kg/m),		WTm =	99.7	kg/m	단위중량(kg/m)
Ring Weight, Shell(1) 제외 중량		WT =	621.6	kg	Ring 1 PCS 중량(kg)

double GET_I( 0.5, 9.86, 0.5, 6.0, 0.5, 4.0, 0,0 ) = [28.8025] cm⁴

No.	b	d	A=b*d	y	A*y	h = y-C1	Ah²	Ig=b*d³/12	SKETCH
No.	mm	mm	mm²	mm	mm³	(mm)	mm⁴	mm⁴
2	0.5	6.0	3.0	3.5	10.5	2.02	12.241	9
1	9.86	0.5	4.93	0.25	1.233	-1.23	7.459	0.103
	SUM	∑ =	7.93		11.733		19.7	9.103

C1	= ∑(AY) / ∑(A) (무게중심 위치)	C1 =	1.48	mm	무게중심에서 FLANGE 하단 까지 떨어진 거리
C2	= H - C1	C2 =	5.02	mm	무게중심에서 FLANGE 상단 까지 떨어진 거리
∑(A)	= Sum of Section Area (단면적)	∑(A)=	7.93	mm²	단면적 (빗금전체)
Ix	= ∑(Ah²) + ∑(Ig)	Ix =	28.803	mm⁴	X축 단면2차모멘트 (Moment of inertia)
Zx	= Ix / Max(C1, C2)	Zx =	5.738	mm³	X축 단면계수 (Section Modulus)
Zmax	= Ix / Min(C1, C2)	Zmax =	19.461	mm³	X축 (최대) 단면계수
Rx	= SQRT( Ix / A )	Rx =	1.906	mm	X축 회전반경
Ry	= SQRT( Iy / A )	Ry =	2.246	mm	Y축 회전반경
Section Area(Shell 포함)		Sarea =	7.93	mm²	Section Area(Shell 포함)
Ring 단면적 (Shell 제외)		ARing =	3	mm²	Ring 단면적 (Shell 제외)
Ring 원주길이		Leng =	6.28	m	Ring 길이(m) = 3.141592×(Di-C1)
Ring 단위중량 (kg/m),		WTm =	0	kg/m	단위중량(kg/m)
Ring Weight, Shell(1) 제외 중량		WT =	0	kg	Ring 1 PCS 중량(kg)

double GET_I( 0.5, 9.86, 0.5, 6.0, 0.5, 4.0, 0,0 ) = [73.2108] cm⁴

No.	b	d	A=b*d	y	A*y	h = y-C1	Ah²	Ig=b*d³/12	SKETCH
No.	mm	mm	mm²	mm	mm³	(mm)	mm⁴	mm⁴
3	4.0	0.5	2.0	6.75	13.5	4.209	35.431	0.042
2	0.5	6.0	3.0	3.5	10.5	0.959	2.759	9
Shell	9.86	0.5	4.93	0.25	1.233	-2.291	25.876	0.103
	SUM	∑ =	9.93		25.233		64.066	9.144

C1	= ∑(AY) / ∑(A) (무게중심 위치)	C1 =	2.541	mm	무게중심에서 FLANGE 하단 까지 떨어진 거리
C2	= H - C1	C2 =	4.459	mm	무게중심에서 FLANGE 상단 까지 떨어진 거리
∑(A)	= Sum of Section Area (단면적)	∑(A)=	9.93	mm²	단면적 (빗금전체)
Ix	= ∑(Ah²) + ∑(Ig)	Ix =	73.211	mm⁴	X축 단면2차모멘트 (Moment of inertia)
Zx	= Ix / Max(C1, C2)	Zx =	16.419	mm³	X축 단면계수 (Section Modulus)
Zmax	= Ix / Min(C1, C2)	Zmax =	28.812	mm³	X축 (최대) 단면계수
Rx	= SQRT( Ix / A )	Rx =	2.715	mm	X축 회전반경
Ry	= SQRT( Iy / A )	Ry =	2.073	mm	Y축 회전반경
Section Area(Shell 포함)		Sarea =	9.93	mm²	Section Area(Shell 포함)
Ring 단면적 (Shell 제외)		ARing =	5	mm²	Ring 단면적 (Shell 제외)
Ring 원주길이		Leng =	6.28	m	Ring 길이(m) = 3.141592×(Di-C1)
Ring 단위중량 (kg/m),		WTm =	0	kg/m	단위중량(kg/m)
Ring Weight, Shell(1) 제외 중량		WT =	0	kg	Ring 1 PCS 중량(kg)

double GET_I( 0.5, 9.86, 0.5, 6.0, 0.5, 4.0, 0,0 ) = [103.7471] cm⁴

No.	b	d	A=b*d	y	A*y	h = y-C1	Ah²	Ig=b*d³/12	SKETCH
No.	mm	mm	mm²	mm	mm³	(mm)	mm⁴	mm⁴
3	4.0	0.5	2.0	7.25	14.5	5.306	56.307	0.042
2	0.5	6.0	3.0	4.0	12	2.056	12.681	9
1	9.86	0.5	4.93	0.75	3.698	-1.194	7.028	0.103
Shell	12.86	0.5	6.43	0.25	1.608	-1.694	18.452	0.134
	SUM	∑ =	16.36		31.805		94.469	9.278

C1	= ∑(AY) / ∑(A) (무게중심 위치)	C1 =	1.944	mm	무게중심에서 FLANGE 하단 까지 떨어진 거리
C2	= H - C1	C2 =	5.556	mm	무게중심에서 FLANGE 상단 까지 떨어진 거리
∑(A)	= Sum of Section Area (단면적)	∑(A)=	16.36	mm²	단면적 (빗금전체)
Ix	= ∑(Ah²) + ∑(Ig)	Ix =	103.747	mm⁴	X축 단면2차모멘트 (Moment of inertia)
Zx	= Ix / Max(C1, C2)	Zx =	18.673	mm³	X축 단면계수 (Section Modulus)
Zmax	= Ix / Min(C1, C2)	Zmax =	53.368	mm³	X축 (최대) 단면계수
Rx	= SQRT( Ix / A )	Rx =	2.518	mm	X축 회전반경
Ry	= SQRT( Iy / A )	Ry =	2.833	mm	Y축 회전반경
Section Area(Shell 포함)		Sarea =	16.36	mm²	Section Area(Shell 포함)
Ring 단면적 (Shell 제외)		ARing =	9.93	mm²	Ring 단면적 (Shell 제외)
Ring 원주길이		Leng =	6.28	m	Ring 길이(m) = 3.141592×(Di-C1)
Ring 단위중량 (kg/m),		WTm =	0	kg/m	단위중량(kg/m)
Ring Weight, Shell(1) 제외 중량		WT =	0	kg	Ring 1 PCS 중량(kg)

Pressure Vessel 핸드북(95쪽) 보강링의 관성모멘트(I) 계산식 보기 연습문제
SIZE : [T 60x5+40x5] Shell Size(t1 x w1) = [t5.0 x 98.6 mm]

No.	b	d	A=b*d	y	A*y	h = y-C1	Ah²	Ig=b*d³/12	SKETCH
No.	cm	cm	cm²	cm	cm³	(cm)	cm⁴	cm⁴
2	0.5	6.0	3.0	3.5	10.5	2.02	12.24	9
1	9.86	0.5	4.93	0.25	1.23	-1.23	7.46	0.1
	SUM	∑ =	7.93		11.73		19.7	9.1

C1	= ∑(AY) / ∑(A) (무게중심 위치)	C1 =	1.48	cm	무게중심에서 FLANGE 하단 까지 떨어진 거리
C2	= H - C1	C2 =	5.02	cm	무게중심에서 FLANGE 상단 까지 떨어진 거리
∑(A)	= Sum of Section Area (단면적)	∑(A)=	7.93	cm²	단면적 (빗금전체)
Ix	= ∑(Ah²) + ∑(Ig)	Ix =	28.8	cm⁴	X축 단면2차모멘트 (Moment of inertia)
Zx	= Ix / Max(C1, C2)	Zx =	5.74	cm³	X축 단면계수 (Section Modulus)
Zmax	= Ix / Min(C1, C2)	Zmax =	19.46	cm³	X축 (최대) 단면계수
Rx	= SQRT( Ix / A )	Rx =	1.91	cm	X축 회전반경
Ry	= SQRT( Iy / A )	Ry =	2.25	cm	Y축 회전반경
Section Area(Shell 포함)		Sarea =	7.93	cm²	Section Area(Shell 포함)
Ring 단면적 (Shell 제외)		ARing =	3	cm²	Ring 단면적 (Shell 제외)
Ring 원주길이		Leng =	6.28	m	Ring 길이(m) = 3.141592×(Di-C1)
Ring 단위중량 (kg/m),		WTm =	2.36	kg/m	단위중량(kg/m)
Ring Weight, Shell(1) 제외 중량		WT =	14.8	kg	Ring 1 PCS 중량(kg)

Dynamic Pressure Calculation

(IGC 4.28.2.1) The following formulae are given as guidance for the components of acceleration
due to ship's motions corresponding to a probability level of 10-8 in the North Atlantic
and apply to ships with a length exceeding 50 m and at or near their service speed:
ρ = maximum liquefied gas fuel density (kg/m³) at the design temperature.

Design parameter of ship motion :

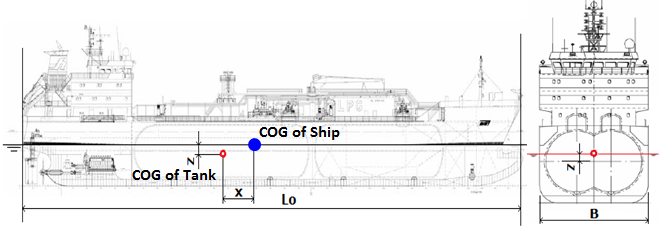Lo = length of the ship for determination of scantlings as defined in 　　　recognized standards (m); 선박의 최대 길이	Lo =	132.0	m
B = greatest moulded breadth of the ship (m); 선박의 최대 폭	B =	23.0	m
x = longitudinal distance (m) from amidships to the centre of gravity of 　　　the tank with contents; x is positive forward of amidships, negative 　　　aft of amidships; 선박의 중앙 에서 Tank 의 중심까지 거리, 선수방향을 정(+), 선미방향을 부(-)	x =	-50.0	m
y = transverse distance (m) from centreline to the centre of gravity of 　　　the tank with contents; 선박의 횡방향 중앙에서 Tank 의 중심까지 떨어진 거리	y =	0.0	m
z = vertical distance (m) from the ship's actual waterline to the centre 　　　of gravity of tank with contents; z is positive above and negative 　　　below the waterline; 선박의 흘수선에서 Tank 의 중심까지 높이, 홀수선상으로부터 상을 정(+), 하를 부(-)	z =	7.0	m
CB = block coefficient; [help]	CB =	0.787
K = 1 in general. For particular loading conditions and hull forms, 　　　determination of K according to the following formula may be necessary; 　　　K = 13*GM/B, where K ≥ 1 and GM = metacentric height, GM = 1 (m);	K =	1.9
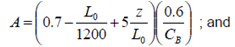	A =	0.652
V = service speed (knots);	V =	12.0	knots
Acceleration due to ship's motions :
	az =	0.7190	g
	ay =	0.8977	g
	ax =	0.2452	g
	a₀ =	0.4320	g

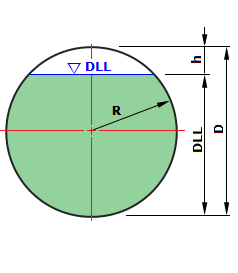
1. Design Data
Description	Symbol	Cylinder	BI-LOBE	Unit
Tank Dia.	D =	7100		mm
Design Liquiod level	DLL =	7100		mm
Radius of tank	R =	3550		mm
Tank center to Swash Bulk Head (For Bilobe)	C =	0	0	mm
Dimension x, (Tank T.L to T.L)	x =	23000		mm
Dimension y	y =	0		mm
Dimension z, z = DLL - R	z =	3550		mm
Tank Total Length	L=2R+x	30100		mm
2. Internal liquid pressure calculation [ as per IGC CODE]
Design Internal pressure ( Design Data )	Po =	4.5		bar.g
MARVS ( Design Data )	MARVS =	4.5		bar.g
Internal liquid pressure ( Calculated IGC CODE ) 　　 Pgd(max) = Max(Pgd_x, Pgd_y)	Pgd(max) =	0.7248		bar.g
Total Design Pressure : Peq = Po + (Pgd)max	Peq =	5.2248		bar.g
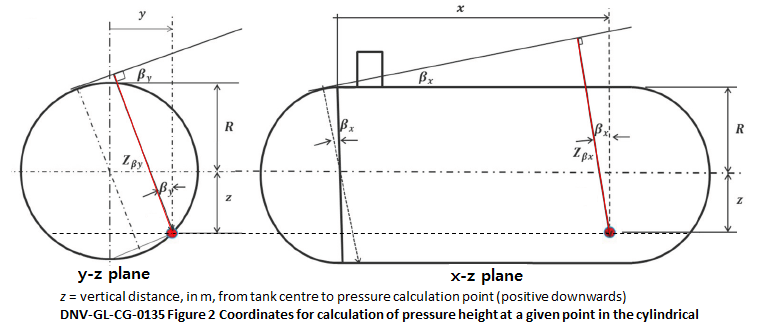
Description	Symbol	Y-Z plane	X-Z plane	Unit
Pgd : Internal liquid pressure ( IGC 4.28.1.2 ) 　　　　*Pgd = a_β* · Z_β · ( ρ / 10^-4 )** [bar.g]	Pgd =	0.5983	0.7248	bar.g
ρ : Design Density of LNG	ρ =	500	500	kg/m³
a_β : dimensionless acceleration, resulting from gravitational 　　　　　and dynamic loads in an arbitrary direction β	a_β =	1.7190	1.4931	g
Z_β : largest liquid height (m) above the point where the pressure is to be determined 　　　　　measured from the Tank shell in the β direction	Z_β =	7.100	9.903	m
β : angles of resulting acceleration vector in relative to the vertical plane	β =	0	7	deg.
βmax : maximum angle (Full Loading Condition)	βmax =	52.253	19.433	deg.
β = βmax(FWD) : Maximum angle (Collision Crash Stop), ax = 0.5g 　β = βmax(AFD) : Maximum angle (Collision Crash Stop), ax = -0.25g	βmax =		26.565 14.036	deg. deg.

3.1 Dynamic Pressure Calculation Result (Max. Accelation and Max. Pgd(Max)
Sloshing Load Calculation (Full loading)								Collision Crash Stop(FWD) ax = 0.5g				Collision Crash Stop(AFD) ax =－0.25g
Transverse (y-z plane)				Longitudinal (x-z plane)				Longitudinal (x-z plane)				Longitudinal (x-z plane)
β (deg)	aβ (g)	Zβ (m)	Pgd (bar.g)	β (deg)	aβ (g)	Zβ (m)	Pgd (bar.g)	β (deg)	aβ (g)	Zβ (m)	Pgd (bar.g)	β (deg)	aβ (g)	Zβ (m)	Pgd (bar.g)
0	1.7190	7.1000	0.5983	7	1.4931	9.9030	0.7248	26.565	1.1180	17.3859	0.9528	14.036	1.0308	12.6782	0.6406

3.2 Dynamic Pressure Calculation by Each Angle
Sloshing Load Calculation (Full loading)								Collision Crash Stop(FWD) ax = 0.5g				Collision Crash Stop(AFD) ax =－0.25g
(측면) Transverse (y-z plane)				(길이) Longitudinal (x-z plane)				(길이) Longitudinal (x-z plane)				(길이) Longitudinal (x-z plane)
β (deg)	aβ (g)	Zβ (m)	Pgd (bar.g)	β (deg)	aβ (g)	Zβ (m)	Pgd (bar.g)	β (deg)	aβ (g)	Zβ (m)	Pgd (bar.g)	β (deg)	aβ (g)	Zβ (m)	Pgd (bar.g)
0	1.7190	7.100	0.5983	0	1.7190	7.100	0.5983	0	1.0000	7.100	0.3480	0	1.0000	7.100	0.3480
1	1.7189	7.100	0.5982	1	1.7139	7.501	0.6302	1	1.0002	7.501	0.3678	1	1.0002	7.501	0.3678
2	1.7184	7.100	0.5981	2	1.6987	7.903	0.6581	2	1.0006	7.903	0.3876	2	1.0006	7.903	0.3876
3	1.7177	7.100	0.5978	3	1.6738	8.304	0.6813	3	1.0014	8.304	0.4076	3	1.0014	8.304	0.4076
4	1.7168	7.100	0.5975	4	1.6399	8.704	0.6997	4	1.0024	8.704	0.4277	4	1.0024	8.704	0.4277
5	1.7155	7.100	0.5971	5	1.5979	9.105	0.7131	5	1.0038	9.105	0.4480	5	1.0038	9.105	0.4480
6	1.7139	7.100	0.5965	6	1.5486	9.504	0.7215	6	1.0055	9.504	0.4685	6	1.0055	9.504	0.4685
7	1.7121	7.100	0.5959	7	1.4931	9.903	0.7248	7	1.0075	9.903	0.4891	7	1.0075	9.903	0.4891
8	1.7099	7.100	0.5951	8	1.4325	10.301	0.7233	8	1.0098	10.301	0.5099	8	1.0098	10.301	0.5099
9	1.7075	7.100	0.5943	9	1.3679	10.698	0.7173	9	1.0125	10.698	0.5310	9	1.0125	10.698	0.5310
10	1.7047	7.100	0.5933	10	1.3002	11.094	0.7071	10	1.0154	11.094	0.5522	10	1.0154	11.094	0.5522
11	1.7016	7.100	0.5922	11	1.2303	11.489	0.6929	11	1.0187	11.489	0.5737	11	1.0187	11.489	0.5737
12	1.6982	7.100	0.5910	12	1.1588	11.882	0.6749	12	1.0223	11.882	0.5954	12	1.0223	11.882	0.5954
13	1.6944	7.100	0.5897	13	1.0864	12.274	0.6536	13	1.0263	12.274	0.6175	13	1.0263	12.274	0.6175
14	1.6901	7.100	0.5882	14	1.0106	12.678	0.6281	14	1.0308	12.678	0.6406	14.036	1.0308	12.678	0.6406
15	1.6858	7.100	0.5867	15	0.9395	13.053	0.6011	15	1.0353	13.053	0.6624
16	1.6809	7.100	0.5850	16	0.8647	13.440	0.5697	16	1.0403	13.440	0.6854
17	1.6757	7.100	0.5832	17	0.7878	13.824	0.5339	17	1.0457	13.824	0.7086
18	1.6700	7.100	0.5812	18	0.7056	14.207	0.4914	18	1.0515	14.207	0.7323
19	1.6640	7.100	0.5791	19.433	0.6058	14.588	0.4332	19	1.0576	14.588	0.7563
20	1.6575	7.100	0.5769					20	1.0642	14.966	0.7808
21	1.6505	7.100	0.5744					21	1.0711	15.342	0.8056
22	1.6430	7.100	0.5718					22	1.0785	15.716	0.8309
23	1.6351	7.100	0.5691					23	1.0864	16.087	0.8567
24	1.6266	7.100	0.5661					24	1.0946	16.455	0.8829
25	1.6176	7.100	0.5630					25	1.1034	16.820	0.9098
26	1.6023	7.100	0.5577					26.565	1.1180	17.386	0.9528
27	1.5977	7.100	0.5561
28	1.5869	7.100	0.5523
29	1.5754	7.100	0.5483
30	1.5631	7.100	0.5440
31	1.5501	7.100	0.5395
32	1.5364	7.100	0.5347
33	1.5217	7.100	0.5296
34	1.5062	7.100	0.5242
35	1.4898	7.100	0.5185
36	1.4723	7.100	0.5124
37	1.4538	7.100	0.5060
38	1.4341	7.100	0.4991
39	1.4131	7.100	0.4918
40	1.3908	7.100	0.4841
41	1.3670	7.100	0.4758
42	1.3416	7.100	0.4669
43	1.3144	7.100	0.4575
44	1.2851	7.100	0.4473
45	1.2536	7.100	0.4363
46	1.2194	7.100	0.4244
47	1.1820	7.100	0.4114
48	1.1406	7.100	0.3970
49	1.0939	7.100	0.3807
50	1.0397	7.100	0.3619
51	0.9725	7.100	0.3385
52.253	0.8684	7.100	0.3022

3. Tank 용량별 Dia. 비교표

구분	Hemi-Spherical Vessel						2:1 Ellipsoidal Head Vessel						10% Dish-Head Vessel

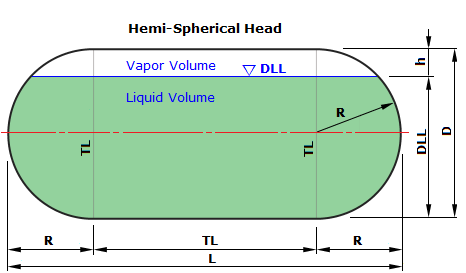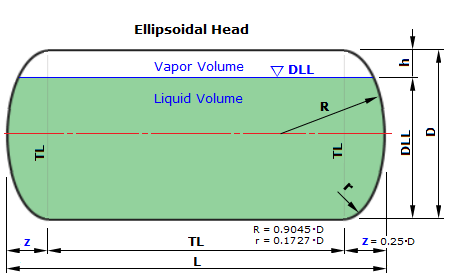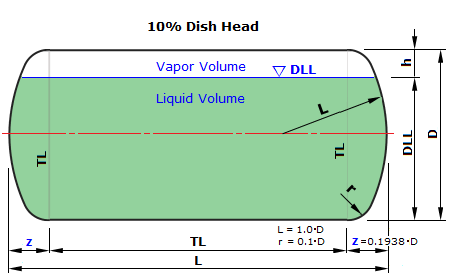	R = 0.5×D,　　Vnom = π×[(D³/ 6) ＋ (D²× L / 4)]						R = 0.9045×D,　r = 0.172744×D,　z = 0.25×D,　Vnom = (π×D³/12) ＋ (L×π×D²/4)						L = 1.0×D,　r = 0.1×D,　z=0.193774×D,　C=0.3780223,　Vnom = (2×C×π×D³/12) ＋ (L×π×D²/4)
번호	Dia (m)	TL TO TL Length (m)	Head End to End Length (m)	1) HEAD Volume(m)	2) Cylinder Volume(m)	3) 공칭용량 Total Volume(m)	Dia (m)	TL TO TL Length (m)	Head End to End Length (m)	1) HEAD Volume(m)	2) Cylinder Volume(m)	3) 공칭용량 Total Volume(m)	Dia (m)	TL TO TL Length (m)	Head End to End Length (m)	1) HEAD Volume(m)	2) Cylinder Volume(m)	3) 공칭용량 Total Volume(m)
1	12.500	40.267	52.767	1022.654	4941.463	5964.117	12.500	44.433	50.683	511.327	5452.790	5964.117	12.500	45.450	50.175	386.586	5577.531	5964.117
2	12.600	39.432	52.032	1047.394	4916.723	5964.117	12.600	43.632	49.932	523.697	5440.420	5964.117	12.600	44.656	49.419	395.938	5568.179	5964.117
3	12.700	38.615	51.315	1072.531	4891.586	5964.117	12.700	42.848	49.198	536.265	5427.852	5964.117	12.700	43.881	48.682	405.441	5558.676	5964.117
4	12.800	37.815	50.615	1098.066	4866.051	5964.117	12.800	42.082	48.482	549.033	5415.084	5964.117	12.800	43.123	47.961	415.094	5549.023	5964.117
5	12.900	37.033	49.933	1124.004	4840.113	5964.117	12.900	41.333	47.783	562.002	5402.115	5964.117	12.900	42.382	47.258	424.898	5539.219	5964.117
6	13.000	36.267	49.267	1150.347	4813.770	5964.117	13.000	40.600	47.100	575.173	5388.944	5964.117	13.000	41.657	46.572	434.857	5529.260	5964.117
7	13.100	35.517	48.617	1177.098	4787.019	5964.117	13.100	39.883	46.433	588.549	5375.568	5964.117	13.100	40.949	45.901	444.969	5519.148	5964.117
8	13.200	34.782	47.982	1204.260	4759.857	5964.117	13.200	39.182	45.782	602.130	5361.987	5964.117	13.200	40.256	45.245	455.237	5508.880	5964.117
9	13.300	34.063	47.363	1231.838	4732.279	5964.117	13.300	38.496	45.146	615.919	5348.198	5964.117	13.300	39.577	44.605	465.662	5498.455	5964.117
10	13.400	33.358	46.758	1259.833	4704.284	5964.117	13.400	37.824	44.524	629.917	5334.200	5964.117	13.400	38.914	43.979	476.245	5487.872	5964.117
11	13.500	32.667	46.167	1288.249	4675.868	5964.117	13.500	37.167	43.917	644.125	5319.992	5964.117	13.500	38.264	43.368	486.987	5477.130	5964.117
12	13.600	31.990	45.590	1317.090	4647.027	5964.117	13.600	36.523	43.323	658.545	5305.572	5964.117	13.600	37.629	42.770	497.889	5466.228	5964.117
13	13.700	31.326	45.026	1346.357	4617.760	5964.117	13.700	35.892	42.742	673.179	5290.938	5964.117	13.700	37.006	42.185	508.953	5455.164	5964.117
14	13.800	30.675	44.475	1376.055	4588.062	5964.117	13.800	35.275	42.175	688.028	5276.089	5964.117	13.800	36.397	41.614	520.180	5443.937	5964.117
15	13.900	30.036	43.936	1406.187	4557.930	5964.117	13.900	34.670	41.620	703.093	5261.024	5964.117	13.900	35.800	41.055	531.570	5432.547	5964.117
16	14.000	29.410	43.410	1436.755	4527.362	5964.117	14.000	34.077	41.077	718.378	5245.739	5964.117	14.000	35.215	40.508	543.125	5420.992	5964.117
17	14.100	28.796	42.896	1467.763	4496.354	5964.117	14.100	33.496	40.546	733.882	5230.235	5964.117	14.100	34.643	39.973	554.847	5409.270	5964.117
18	14.200	28.193	42.393	1499.214	4464.903	5964.117	14.200	32.927	40.027	749.607	5214.510	5964.117	14.200	34.081	39.449	566.736	5397.381	5964.117
19	14.300	27.602	41.902	1531.111	4433.006	5964.117	14.300	32.368	39.518	765.556	5198.561	5964.117	14.300	33.531	38.937	578.794	5385.323	5964.117
20	14.400	27.021	41.421	1563.458	4400.659	5964.117	14.400	31.821	39.021	781.729	5182.388	5964.117	14.400	32.992	38.436	591.022	5373.095	5964.117
21	14.500	26.451	40.951	1596.256	4367.861	5964.117	14.500	31.284	38.534	798.128	5165.989	5964.117	14.500	32.463	37.945	603.420	5360.697	5964.117

유튜브 보기

	
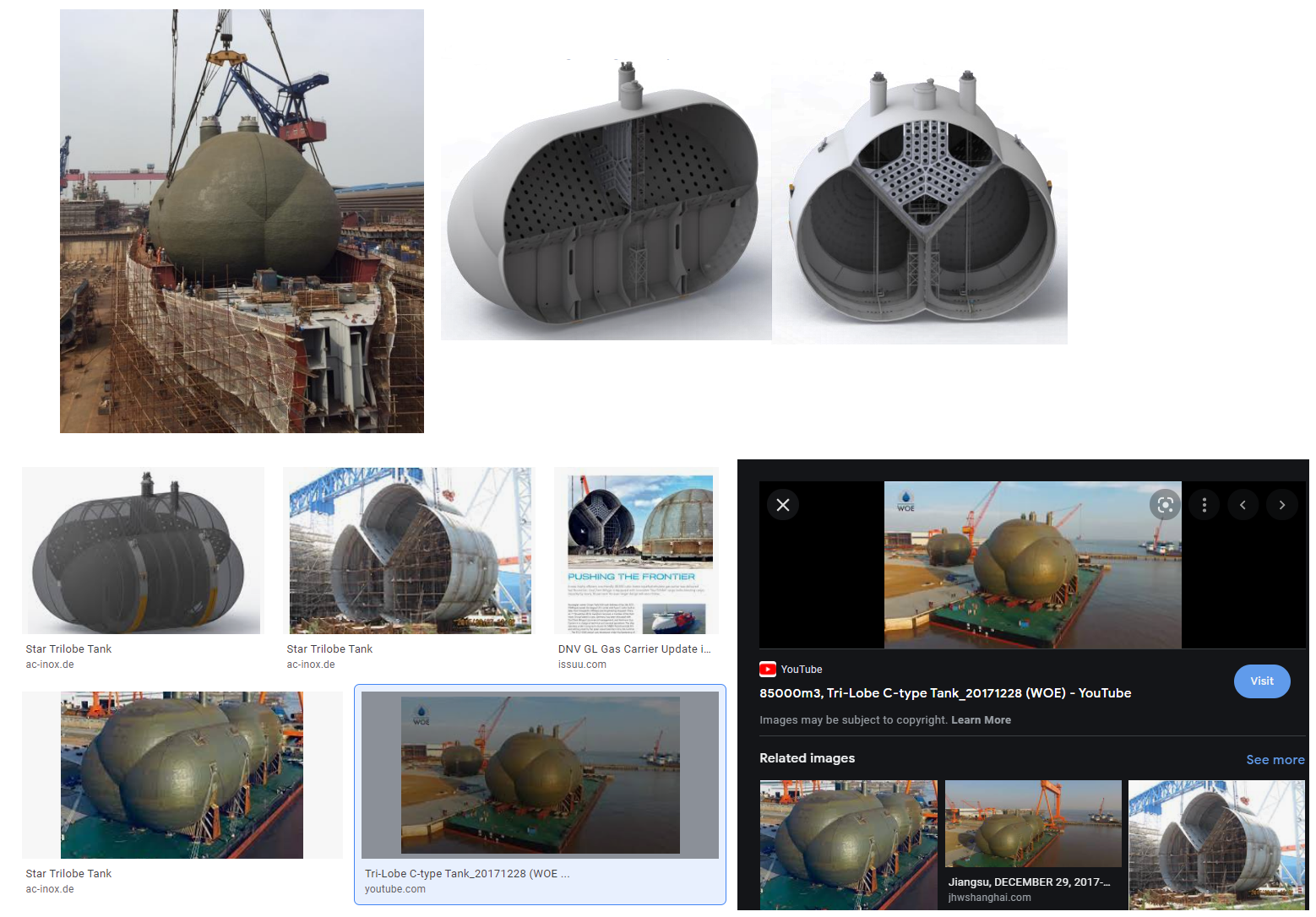
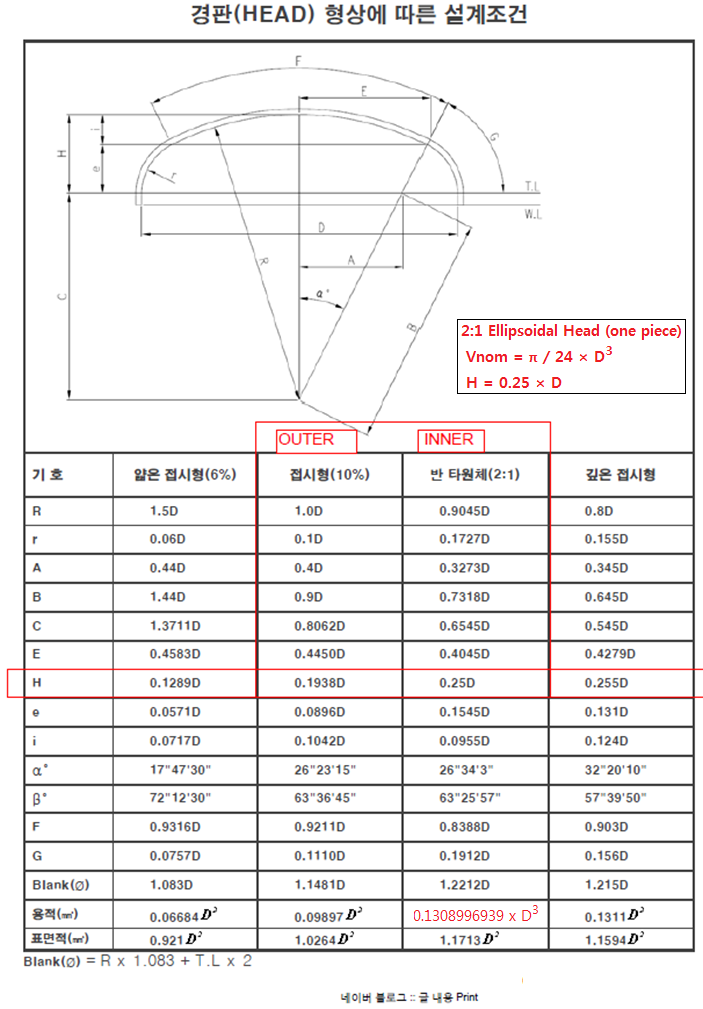
	var Di  = 2210;
	var Ri  = Di / 2;
	var DLL = 1853;

	var z = 552.5 ; 
	var C = 2 * 552.5 / 2210;
	C	= 0.5;
      
    var V_one_head = Math.pow(Di,3) * C * ( Math.PI / 12) * ( 3 * Math.pow((DLL / Di ),2) - 2 * Math.pow((DLL/Di),3));
	var V_Cylinder = L * ( Ri^2 * Math.acos((Ri-DLL)/Ri) - (Ri - DLL) * Math.sqrt(Di * DLL - Math.pow(DLL,2)));

	var V = V_one_head + V_Cylinder;

	https://stackoverflow.com/questions/2172798/how-to-draw-an-oval-in-html5-canvas	
	There doesnt seem to be a native function to draw an oval-like shape. Also i am not looking for the egg-shape.
	Is it possible to draw an oval with 2 bezier curves? Somebody expierenced with that?
	My purpose is to draw some eyes and actually im just using arcs. Thanks in advance. Solution
	So scale() changes the scaling for all next shapes. Save() saves the settings before and restore is used to restore the settings to draw new shapes without scaling.
	Thanks to Jani
	
	ctx.save();
	ctx.scale(0.75, 1);
	ctx.beginPath();
	ctx.arc(20, 21, 10, 0, Math.PI*2, false);
	ctx.stroke();
	ctx.closePath();
	ctx.restore();

시작시간 = [2024-12-05 00:59:19.0607]
종료시간 = [2024-12-05 00:59:19.0612]

PRT_IMO_FORMULA_BUNSU() / FUNCTION_MATH.jsp 에 있음 출처 : ASME SHELL THICKNESS CALCULATION 출처

Wall thickness calculation of Sphere
according ASME

Allowable stress

S =

175.2 =

175.20 N/mm²

Corroded thickness

t_c = t - Ca - tol =

8.2 - 1 - 1.03 =

6.17 mm

Sphere:

Corroded inside radius

D_o

- t_c=

219.1

- 6.17 =

103.38 mm

Cylinder Shell : ＋－×÷
Required wall thickness

t_r

P · R
S×E － 0.6×P

＋ CA

0.5 × 103.38

2 × 175.2 × 1.0 － 0.2 × 0.5

＋ CA

0.15 mm

Spherical Head :
Required wall thickness

t_r

P · R
2SE － 0.2P

＋ CA

0.5 × 103.38

2 × 175.2 × 1.0 － 0.2 × 0.5

＋ CA

0.15 mm

2:1 Ellipsoidal Head :
Required wall thickness

t_r

P ⋅ D
2 ⋅ S ⋅ E - 0.2 ⋅ P

+ CA

0.5 * 103.38

2 * 175.2 * 1.0 - 0.2 * 0.5

+ CA

0.15 mm

10% Dish Head :
Required wall thickness

t_r

P ⋅ D ⋅ K
2 * S * E - 0.2 * P

+ CA

0.5 * 103.38

2 * 175.2 * 1.0 - 0.2 * 0.5

+ CA

0.15 mm

Nominal required thickness

t_rn = t_r + Ca + tol =

0.148 + 1 + 1.03 =

2.18 mm

Max. Allowable Working Press.

MAWP

2 ⋅S ⋅ E ⋅ t_c

R + 0.2 ⋅ t_c

2 ⋅ 175.2 ⋅ 1 ⋅ 6.17

103.38 + 0.2 ⋅ 6.17

20.67 N/mm²

Thickness analysis, t > t_rn ?

t = 8.2 mm is OK

Weight

9.00 kg

Enclosed volume

0.004 m³

출처 : 이미지를 캔버스에 넣은후 캔버스 이미지를 로칼스트리지에 저장하는 방법 (바로가기 누르세요)
[바로가기]
테스트 하기 (누르세요)

HTML에서 LATEX Math Library 수식 표현하기 https://www.scientificpsychic.com/etc/square-root.html
네이버 블로그 / HTML에서 수식 표현하기 https://blog.daum.net/asfreeas/18314217

	_______
√	X² + 1

−b ± √ b² − 4ac

HTML 특수문자 리스트

Α α	αλφα	Alpha (알파) 한국어 '아' (영어 cup 의 u 또는 calm 의 a)
Β β	βητα	Beta (베타) 영어 b
Γ γ	γαμμα	Gamma (감마) 영어 get 의 g
Δ δ	δελτα	Delta (델타) 영어 d
Ε ε	εψιλον	Epsilon (엡실론) 한국어 짧은 '에' (영어 bed 의 e)
Ζ ζ	ζετα	Zeta (제타) 영어 zd (나중에 z 로 바뀜)
Η η	ητα	Eta (에타) 한국어 긴 '에' (영어 play 의 ay)
Θ θ	θητα	Theta (세타) 한국어 'ㅌ' (나중에 영어 thank 의 th 로 바뀜)
Ι ι	ιωτα	Iota (이오타) 한국어 '이' (영어 fit 의 i 또는 feet 의 ee)
Κ κ	καππα	Kappa (카파) 한국어 'ㄲ' (영어 k)
Λ λ	λαμβδα	Lambda (람다) 영어 l
Μ μ	μυ	Mu (뮤) 영어 m
Ν ν	νυ	Nu (뉴) 영어 n
Ξ ξ	Ξ ξ	Xi (크사이) 영어 box 의 x
Ο ο	ομικρον	Omicron (오미크론) 한국어 '오' (영국영어 pot 의 o)
Π π	πι	Pi (파이) 한국어 'ㅃ' (영어 p)
Ρ ρ	ρω	Rho (로우) 한국어 '사랑' 의 'ㄹ' (영어 r)
Σ σ	σιγμα	Sigma (시그마) 영어 sing 의 s 시그마의 소문자는 위와 같이 두 가지입니다. 첫 번째는 단어 중간에 올 때 쓰이고 두 번째는 단어 끝에 올 때 쓰입니다.
Τ τ	ταυ	Tau (타우) 영어 t (한국어 된소리 'ㄸ')
Υ υ	υψιλον	Upsilon (웁실론) 프랑스어 u (한국어 '위' 와 비슷) 또는 영어 u
Φ φ	φι	Phi (파이) 한국어 'ㅍ' (나중에 영어 f 로 바뀜)
Χ χ	χι	카이 (xhi) 한국어 'ㅋ' (나중에 독일어 Buch 의 ch 로 바뀜)
Ψ ψ	ψι	프사이 (psi) 영어 ps
Ω ω	ωμεγα	Omega (오메가) 한국어 '오' (영어 tone 의 o)
α ι	αυ	영어 high 의 이중모음과 같습니다. 영어 how 의 이중모음과 같습니다.
ε ι	ευ, ηυ	한국어 '에' 보다 조금 긴 소리입니다. 한국어 '에' 와 '우' 를 각각 발음합니다.
ο ι	ο ι	영어 boy 의 이중모음과 같습니다.
ο υ	ο υ	영어 too 의 장모음과 같습니다.
υ ι	υ ι	영어 quit 의 ui 소리와 같습니다.
γ γ	γ γ	영어 finger 의 ng 발음입니다.
다른 자음들이 이중으로 나타나면 각각을 발음합니다.

HTML 특수문자 리스트

출처 : http://kor.pe.kr/util/4/charmap2.htm

HTML 상에서 특수문자가 제대로 나타나지 않을 수 있기 때문에 아래 문자들를 사용합니다.
표현문자	숫자표현	문자표현	설명
-	-	-	사용하지 않음
space		-	수평탭
space		-	줄 삽입
-	-	-	사용하지 않음
space		-	여백
!	!	-	느낌표
\"	"	"	따옴표
#	#	-	숫자기호
$	$	-	달러
%	%	-	백분율 기호
&	&	&	Ampersand
'	'	-	작은 따옴표
(	(	-	왼쪽 괄호
)	)	-	오른쪽 괄호
*	*	-	아스트릭
+	+	-	더하기 기호
,	,	-	쉼표
-	-	-	Hyphen
.	.	-	마침표
/	/	-	Solidus (slash)
0 - 9	0-9	-	0부터 9까지
:	:	-	콜론
;	;	-	세미콜론
<	<	<	보다 작은
=	=	-	등호
>	>	>	보다 큰
?	?	-	물음표
@	@	-	Commercial at
A - Z	A-Z	-	A부터 Z까지
[	[	-	왼쪽 대괄호
\	\	-	역슬래쉬
]	]	-	오른쪽 대괄호
^	^	-	탈자부호
_	_	-	수평선
`	`	-	Acute accent
a - z	a-z	-	a부터 z까지
{	{	-	왼쪽 중괄호
\|	\|	-	수직선
}	}	-	오른쪽 중괄호
~	~	-	꼬리표
-	-	-	사용하지 않음
			Non-breaking space
¡	¡	¡	거꾸로된 느낌표
￠	¢	¢	센트 기호
￡	£	£	파운드
¤	¤	¤	현재 환율
￥	¥	¥	엔
\|	¦	¦	끊어진 수직선
§	§	§	섹션 기호
¨	¨	¨	움라우트
ⓒ	©	©	저작권
ª	ª	ª	Feminine ordinal
≪	«	«	왼쪽 꺾인 괄호
￢	¬	¬	부정
			Soft hyphen
?	®	®	등록상표
&hibar;	¯	¯	Macron accent
°	°	°	Degree sign
±	±	±	Plus or minus
²	²	²	Superscript two
³	³	³	Superscript three
´	´	´	Acute accent
μ	µ	µ	Micro sign (Mu)
¶	¶	¶	문단기호
·	·	·	Middle dot
¸	¸	¸	Cedilla
¹	¹	¹	Superscript one
º	º	º	Masculine ordinal
≫	»	»	오른쪽 꺾인 괄호
¼	¼	¼	4분의 1
½	½	½	2분의 1
¾	¾	¾	4분의 3
¿	¿	¿	거꾸로된 물음표
	À	À	Capital A, grave accent
	Á	Á	Capital A, acute accent
	Â	Â	Capital A, circumflex accent
	Ã	Ã	Capital A, tilde
	Ä	Ä	Capital A, dieresis or umlaut mark
	Å	Å	Capital A, ring (Angstrom)
Æ	Æ	Æ	Capital AE diphthong (ligature)
C	Ç	Ç	Capital C, cedilla
E	È	È	Capital E, grave accent
E	É	É	Capital E, acute accent
E	Ê	Ê	Capital E, circumflex accent
E	Ë	Ë	Capital E, dieresis or umlaut mark
I	Ì	Ì	Capital I, grave accent
I	Í	Í	Capital I, acute accent
I	Î	Î	Capital I, circumflex accent
I	Ï	Ï	Capital I, dieresis or umlaut mark
Ð	Ð	Ð	Capital Eth, Icelandic
N	Ñ	Ñ	Capital N, tilde
O	Ò	Ò	Capital O, grave accent
O	Ó	Ó	Capital O, acute accent
O	Ô	Ô	Capital O, circumflex accent
O	Õ	Õ	Capital O, tilde
O	Ö	Ö	Capital O, dieresis or umlaut mark
×	×	×	Multiply sign
Ø	Ø	Ø	width=130 Capital O, slash
U	Ù	Ù	Capital U, grave accent
U	Ú	Ú	Capital U, acute accent
U	Û	Û	Capital U, circumflex accent
U	Ü	Ü	Capital U, dieresis or umlaut mark
Y	Ý	Ý	Capital Y, acute accent
Þ	Þ	Þ	Capital Thorn, Icelandic
ß	ß	ß	Small sharp s, German (sz ligature)
	à	à	Small a, grave accent
	á	á	Small a, acute accent
	â	â	Small a, circumflex accent
	ã	ã	Small a, tilde
	ä	ä	Small a, dieresis or umlaut mark
	å	å	Small a, ring
æ	æ	æ	Small ae diphthong (ligature)
c	ç	ç	Small c, cedilla
e	è	è	Small e, grave accent
e	é	é	Small e, acute accent
e	ê	ê	Small e, circumflex accent
e	ë	ë	Small e, dieresis or umlaut mark
i	ì	ì	Small i, grave accent
i	í	í	Small i, acute accent
i	î	î	Small i, circumflex accent
i	ï	ï	Small i, dieresis or umlaut mark
ð	ð	ð	Small eth, Icelandic
n	ñ	ñ	Small n, tilde
o	ò	ò	Small o, grave accent
o	ó	ó	Small o, acute accent
o	ô	ô	Small o, circumflex accent
o	õ	õ	Small o, tilde
o	ö	ö	Small o, dieresis or umlaut mark
÷	÷	÷	Division sign
ø	ø	ø	Small o, slash
u	ù	ù	Small u, grave accent
u	ú	ú	Small u, acute accent
u	û	û	Small u, circumflex accent
u	ü	ü	Small u, dieresis or umlaut mark
y	ý	ý	Small y, acute accent
þ	þ	þ	Small thorn, Icelandic
y	ÿ	ÿ	Small y, dieresis or umlaut mark

HTML END!!!